Explain clearly, with examples, the difference between :
(a) magnitude of displacement (sometimes called distance) over an interval of time, and the total length of the path covered by a particle over the same interval;
(b) magnitude of average velocity over an interval of time, and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval]. Show in both (a) and (b) that the second quantity is either greater than or equal to the first.
When is the equality sing true? [ For simplicity, consider one- dimensional motion only]
(a) The magnitude of displacement over an interval of time is the shortest distance (which is a straight line) between the initial and final positions of the particle.
The total path length of a particle is the actual path length covered by the particle in a given interval of time.
For example, suppose a particle moves from point A to point B and then, comes back to a point, C taking a total time t, as shown below. Then, the magnitude of displacement of the particle = AC.
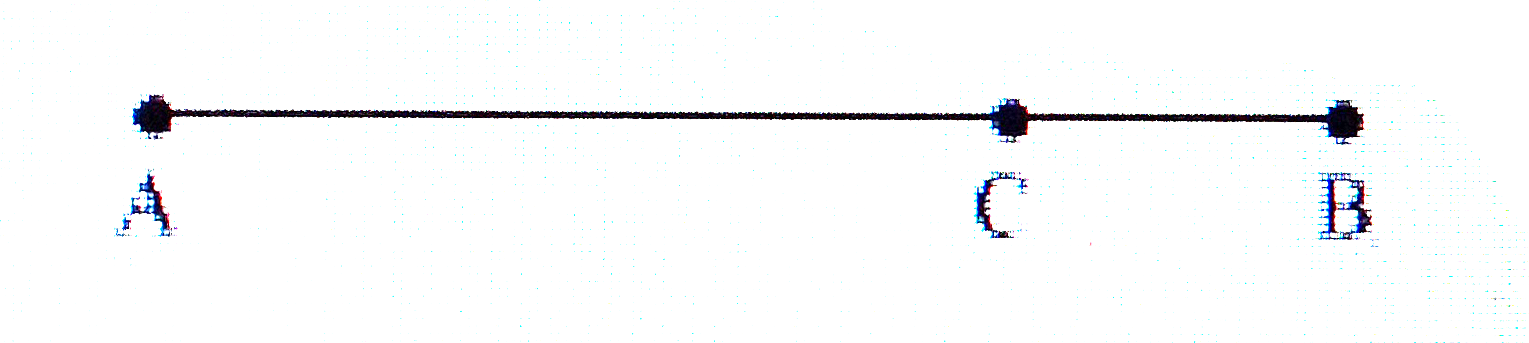
Whereas, total path length = AB + BC
It is also important to note that the magnitude of displacement can never be greater than the total path length. However, in some cases, both quantities are equal to each other.
(b)Magnitude of average velocity =Magnitude of displacementTime interval
For the given particle,
Average velocity =ACt
Average speed =Total path lengthTime interval
=AB+BCt
Since (AB + BC) gt AC, average speed is greater than the magnitude of average velocity. The two quantities will be equal if the particle continues to move along a straight line.
Topper's Solved these Questions
Similar Questions
Explain clearly, with ezamples, the distaintion between :
(a) magnitude of displacemnt (sometimes called distance ) overand interval of time, and the total length of the path coverd by a particle over the same interval.
(b) magnitude of average velocity over an intercal of time , and the average speed ocer the same interval. [ Average speed of a particle over an interval of time is defined as the toal path length divided by the time intrval]. Show in both (a) and (b) that the second quantity is either greater than or equal to first. When is the equality sing true ? [ For simplocity, consider one- dimensional motion only]
View SolutionShow that avertage velocity of the object over an interval of time is either smaller than or equal to the average speed of the object over the same interval.
View Solution
Knowledge Check
It magnitude of average speed and average velocity over an interval of time are same, then
AParticle must move with zero accelerationBParticle must move with uniform accelerationCParticle must be at restDParticle must move in a straight line without turning backIf magnitude of average speed and average velocity over a time interval are same, then
AThe particle must move with zero accelerationBThe particle must move with non-zero accelerationCThe particle must be at restDThe particle must move in a straight line without turning backMagnitude of average velocity and speed are found to be the saame in an interval of time.
AParticle must have zero acceleration.BParticle must have non-zero accelerationCParticle must be moving in a straight line without rebversing the direction of motion.DParticle must be in a state of rest.
Prove that average velocity of an object can never be greater than the average speed of an object over a given interval of time.
View SolutionExplain with example the distinction between the magnitude of average velocity and average speed over the same period. Show that and the average speed is either greater than or equal to the average velocity. When is the equality sign true?
View SolutionFind average speed in time interval t= 2 to t=10s
View SolutionA : The magntidue of average velocity in an interval can never be greater than average speed in that interval.
R : For a moving object distance traveled ≥|Displacement|
View SolutionAssertion: The magnitude of average velocity of the object over an interval of time is either smaller than or equal to the average speed of the object over the same interval.
Reason: Path length (distance) is either equal or greater than the magnitude of displacement.
View Solution
