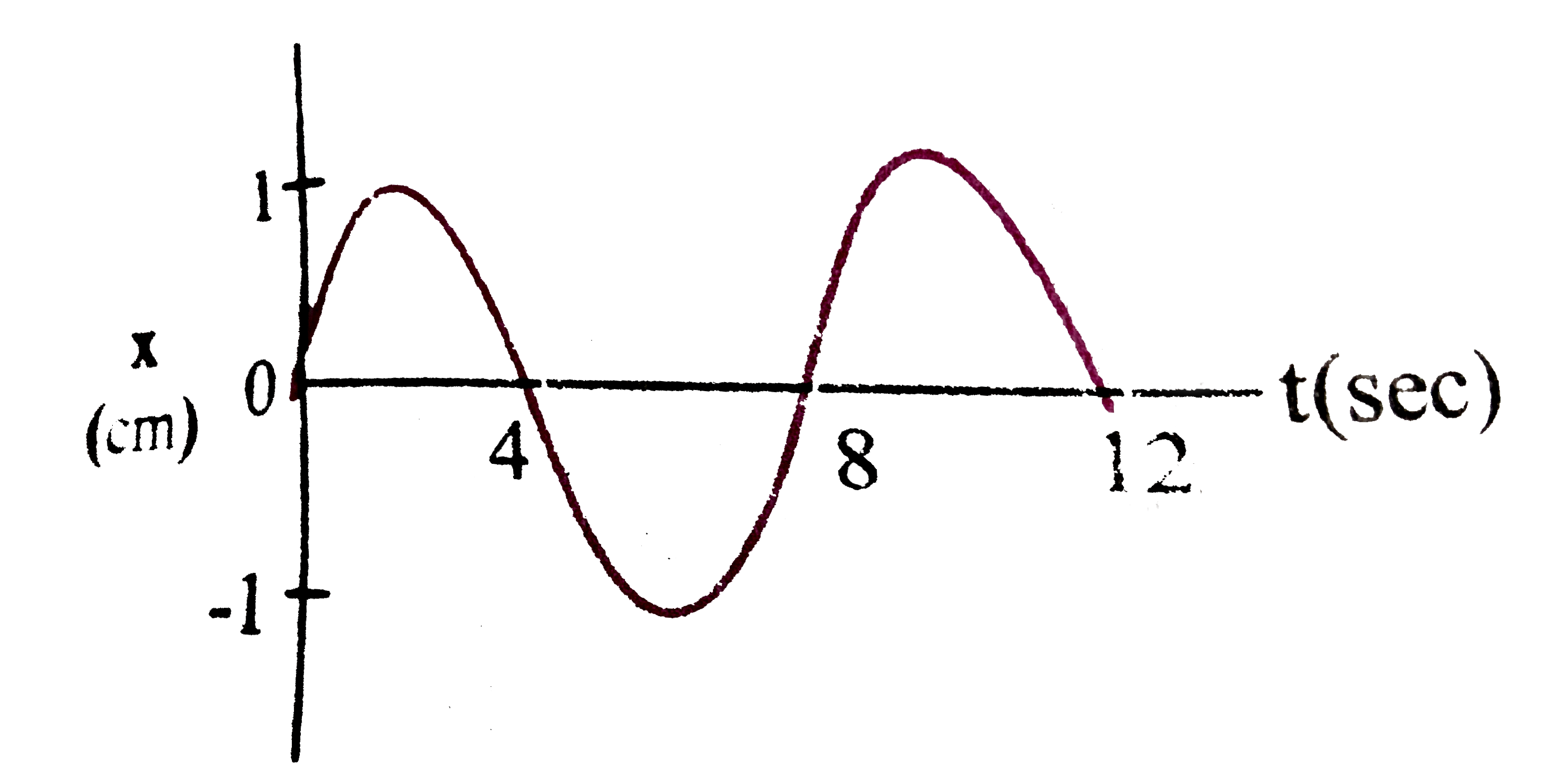
Fig gives the x−t plot of a particle executing one dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particles at t=0.3s, 1.2s,−1.2s,
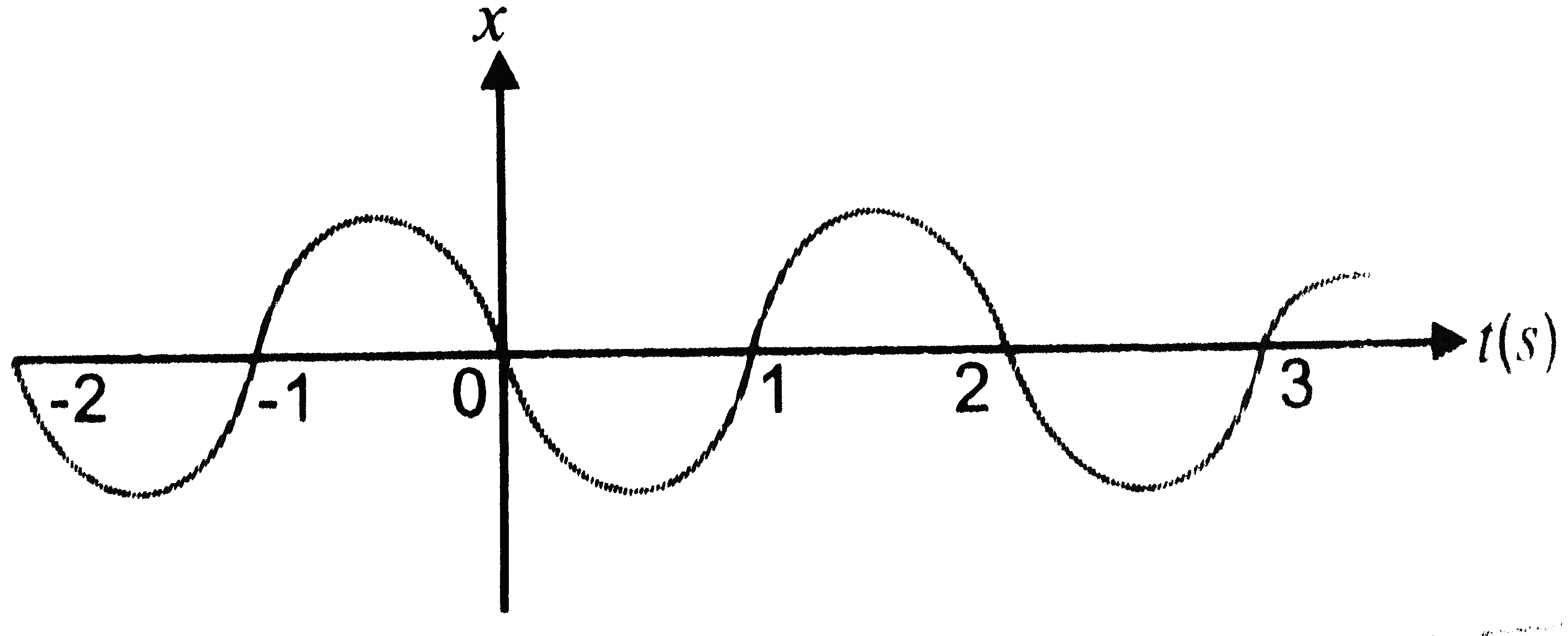
Negative, Negative, Positive (at t = 0.3 s)
Positive, Positive, Negative (at t = 1.2 s)
Negative, Positive, Positive (at t = –1.2 s)
For simple harmonic motion (SHM) of a particle, acceleration (a) is given by the relation:
a=−w2×w→ angular frequency ... (i)
t=0.3 s
In this time interval, x is negative. Thus, the slope of the x-t plot will also be negative. Therefore, both position and velocity are negative. However, using equation (i), acceleration of the particle will be positive.
t = 1.2 s
In this time interval, x is positive. Thus, the slope of the x–t plot will also be positive. Therefore, both position and velocity are positive. However, using equation (i), acceleration of the particle comes to be negative
t = – 1.2 s
In this time interval, x is negative. Thus, the slope of the x–t plot will also be negative. Since both x and t are negative, the velocity comes to be positive. From equation (i), it can be inferred that the acceleration of the particle will be positive.
Topper's Solved these Questions
Similar Questions
Fig 2 (NCT).8 gives the x−t plot of a particle executing one dimensional simle harmonic motion. Give the signs of position, velocity and acceleration variables of the particles at t=0.3s, 1.2s,−1.2s,

View SolutionFigure gives the x-t plot of a particle is one dimensional motion. Give the signs of position, velocity and acceleration of the particle at t = 0.3s

View Solution
Knowledge Check
A particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
A0.5πms−1,0ms−2B0.5ms−1,−5π2ms−2C0ms−1,−5π2ms−2D0.5πms−1,−0.5π2ms−2The x−t graph of a particle undergoing simple harmonic motion is shown below. The accelertion of the particle at t=4/3s is
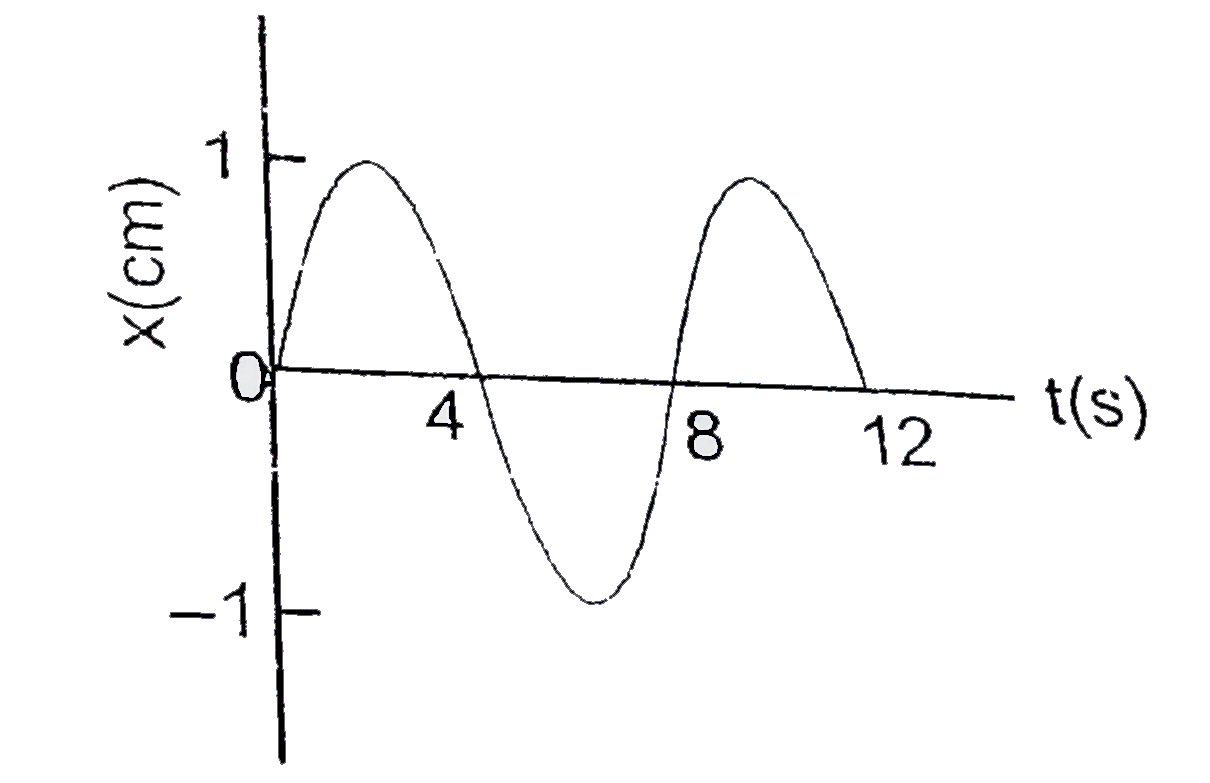 A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle of t=4/3s is
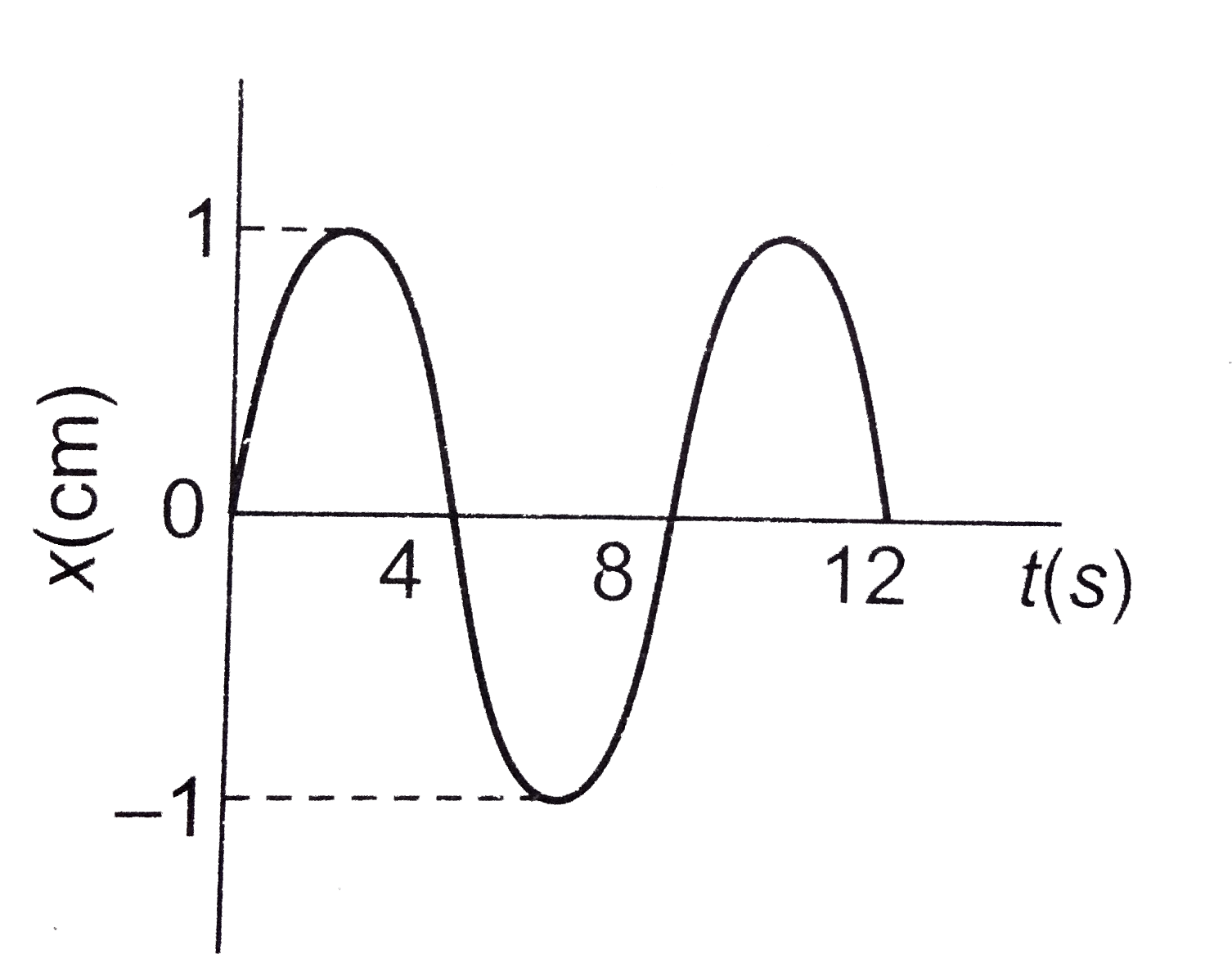 A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t=23s is
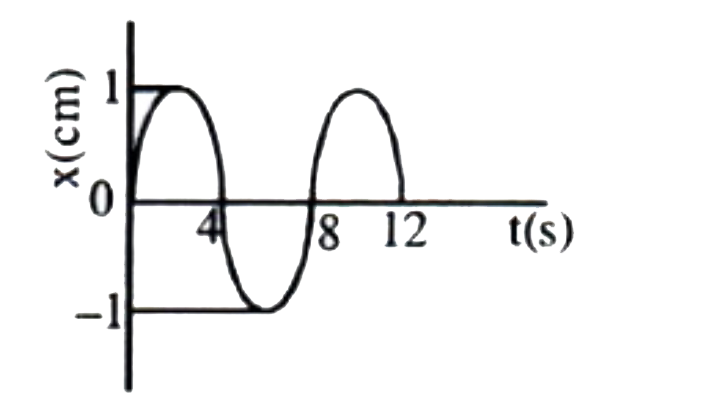
View SolutionIf the motion of aparticle is governed by the equation, s=2t3−3t2+2t+2, find the poswition, velocity and acceleration of the particle at time t=2s.
View SolutionA particle is moving with initial velocity 1m/s and acceleration a=(4t+3)ms2. Find velocity of particle at t=2sec.
View SolutionA particle executes simple harmonic motion with a time period of 16s. At time t=4s its velocity is 4ms−1. Find its amplitute of motion.
View SolutionThe x−t graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at t=4/3s is
View Solution
