Question

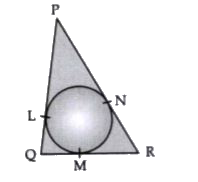
A circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths QM, RN and PL.

Explanation

To find the lengths QM, RN, and PL in triangle PQR with the given side lengths, we can use the property of the incircle of a triangle. The segments created by the points where the incircle touches the sides of the triangle can be expressed in terms of the triangle's sides.

1. Identify the sides of the triangle:
- Let \( PQ = a = 10 \, \text{cm} \)
- Let \( QR = b = 8 \, \text{cm} \)
- Let \( PR = c = 12 \, \text{cm} \)

2. Calculate the semi-perimeter (s):
The semi-perimeter \( s \) of the triangle is given by:
\( s = \frac{a + b + c}{2} = \frac{10 + 8 + 12}{2} = \frac{30}{2} = 15 \, \text{cm} \)

3. Use the semi-perimeter to find the lengths of the segments:
The lengths of the segments from the vertices to the points where the incircle touches the sides are given by:
- \( QM = s - a \)
- \( RN = s - b \)
- \( PL = s - c \)

4. Calculate each segment:
- For \( QM \):
\( QM = s - a = 15 - 10 = 5 \, \text{cm} \)
- For \( RN \):
\( RN = s - b = 15 - 8 = 7 \, \text{cm} \)
- For \( PL \):
\( PL = s - c = 15 - 12 = 3 \, \text{cm} \)

5. Final lengths:
- \( QM = 5 \, \text{cm} \)
- \( RN = 7 \, \text{cm} \)
- \( PL = 3 \, \text{cm} \)

Summary of Results:
- \( QM = 5 \, \text{cm} \)
- \( RN = 7 \, \text{cm} \)
- \( PL = 3 \, \text{cm} \)