In a triangle PQR, right angled at Q. PQ=5 cm, QR=12 cm. Find the length of QM , if M is the mid point of PR .
The correct Answer is:132
To find the length of QM in triangle PQR, which is right-angled at Q, we can follow these steps:
1. Identify the triangle and given values:
- Triangle PQR is right-angled at Q.
- PQ = 5 cm (one leg of the triangle).
- QR = 12 cm (the other leg of the triangle).
2. Use the Pythagorean theorem to find PR:
- According to the Pythagorean theorem, in a right triangle:
PR2=PQ2+QR2
- Substitute the known values:
PR2=52+122
- Calculate the squares:
PR2=25+144
- Add the results:
PR2=169
- Take the square root to find PR:
PR=√169=13 cm
3. Find the length of QM:
- M is the midpoint of PR, so:
PM=MR=PR2
- Substitute the value of PR:
PM=MR=132=6.5 cm
- Since QM is equal to PM (because M is the midpoint), we have:
QM=6.5 cm
Final Answer:
The length of QM is 6.5 cm.
- Triangle PQR is right-angled at Q.
- PQ = 5 cm (one leg of the triangle).
- QR = 12 cm (the other leg of the triangle).
- According to the Pythagorean theorem, in a right triangle:
PR2=PQ2+QR2
- Substitute the known values:
PR2=52+122
- Calculate the squares:
PR2=25+144
- Add the results:
PR2=169
- Take the square root to find PR:
PR=√169=13 cm
- M is the midpoint of PR, so:
PM=MR=PR2
- Substitute the value of PR:
PM=MR=132=6.5 cm
- Since QM is equal to PM (because M is the midpoint), we have:
QM=6.5 cm
The length of QM is 6.5 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In ΔPQR, If ∠R=∠P, QR=4 cm and PR = 5 cm. Then, the length of PQ is
A4 cmB5 cmC2 cmD2.5 cm
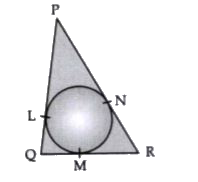
In fig , a circle isinscribed in a triangle PQR with PQ = 10 cm , QR = 8 cm and PR = 12 cm .Find the length of the QM , RN and PL.
View SolutionIn the triangle PQR, C is the centroid. PQ = 30 cm, QR = 36 cm and PR = 50 cm. If D si the midpoint of QR, then what is the length (in cm) of CD?
View SolutionIn ΔPQR right angled at Q , PQ = 3 cm and PR = 6 cm .
Determine side QR.
View SolutionConstruct a triangle PQR such that PQ=6 cm, QR=7cm and PR=4.5cm.
View SolutionConstruct a triangle PQR, such that PQ=38cm, QR=4.3cm and the median from Q to PR is 3.5cm.
View SolutionIn △PQR , right-angled at Q, PQ=3cm and PR=6cm . Determine ∠P and ∠R .
View SolutionIn the given figure, triangle PQR is a right angled triangle at Q. If PQ = 35 cm and QS = 28 cm, then what is the value (in cm) of SR?
View Solution
