A body of mass 2m is connected to another body of mass m as shown in figure. The mass 2m performs vertical S.H.M. Then find out the maximum amplitude of 2m such that mass m doesn't lift up from the ground.
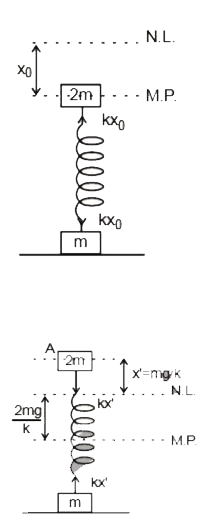
In the given situation 2m mass is in equilibrium condition. Let assume spring is compressed x0 distance from its natural length.
⇒kx0=mg
⇒x0=2mgk
The lower block will be lift up, only in the case when the spring force on it will be greater than equal to mg and in upward direction
⇒ kx' = mg
⇒x'=mgk
Above situation arises when 2m block moves upward mg/k from natural length as shown in figure Block m doesn't lift up if the maximum amplitude of the 2m block is
=2mgk+mgk=3mgk
Topper's Solved these Questions
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-A )
8 Videos
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
23 Videos
- SOUND WAVESBOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 3 (Section - B)
14 Videos
Similar Questions
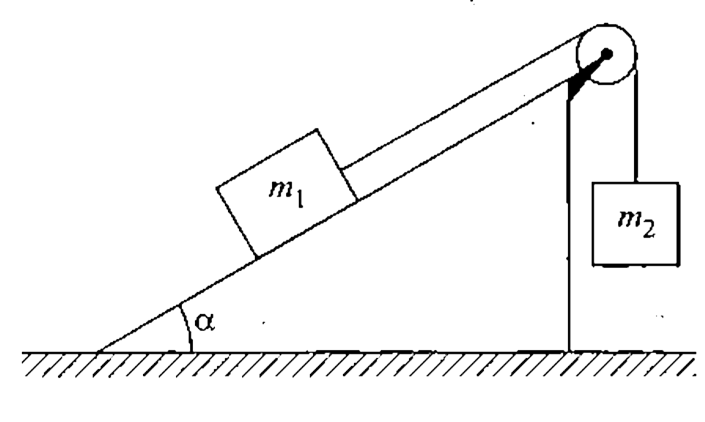
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.

View SolutionFind the acceleration of the prism of mass M and that of the bar of mass m shown in figure.
View Solution
Knowledge Check
A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3KmA body A of mass m1 and body B of mass m2 are interconnected by a massless spring as shown. The body A performs free vertical harmonic oscillations with the amplitude A and frequency f. The maximum value of f such that body B does not leave the surface is
 A12π√(m1+m2m2)gAB12π√(m1+m2m1)gAC12π√gAD12π√m2m1.gA
A12π√(m1+m2m2)gAB12π√(m1+m2m1)gAC12π√gAD12π√m2m1.gAA body of mass m is dropped and another body of mass M is projected vertically up with speed u simultaneously from the top of a tower of height H. If the body reaches the highest piont before the dropped body reaches the ground, then maximum height raised by the centre of mass of the system from ground is
AH+u22gBu22gCH+12g(Mum+M)2DH+12g(mum+M)2
A body A mass m1=1kg and body B of mass m2=4.1kg. The body A perform free vertical harmonic oscillations with the amplitude 1.6cm and frequency 25Hz. Neglecting the mass of the spring , find the maximum and m inimum value of force that the system exerts on the hearing surface.

View SolutionTwo blocks of masses 2m and m are connected by a light string going over a pulley of mass 2m and radius R as shown in the figure. The system is released from rest. Find the angular momentum of system when the mass 2m has descended through a height h. Assume no slipping.

View SolutionA body of mass m moving with velocity v makes a head-on collision with another body of mass 2 m which is initially at rest. The loss of kinetic energy of the colliding body (mass m ) is
View SolutionA body of mass m moving with velocity v makes a head-on collision with another body of mass 2 m which is initially at rest. The loss of kinetic energy of the colliding body (mass m ) is
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View Solution
