A body A mass m1=1kg and body B of mass m2=4.1kg. The body A perform free vertical harmonic oscillations with the amplitude 1.6cm and frequency 25Hz. Neglecting the mass of the spring , find the maximum and m inimum value of force that the system exerts on the hearing surface.

The correct Answer is:(m1+m2)g−m1ω2A
As A oscillates up and down , the normal reation berween B and the surface is maximum , where A is at position and it is minimum when A is at topmost position
Case I: Lowest position of A
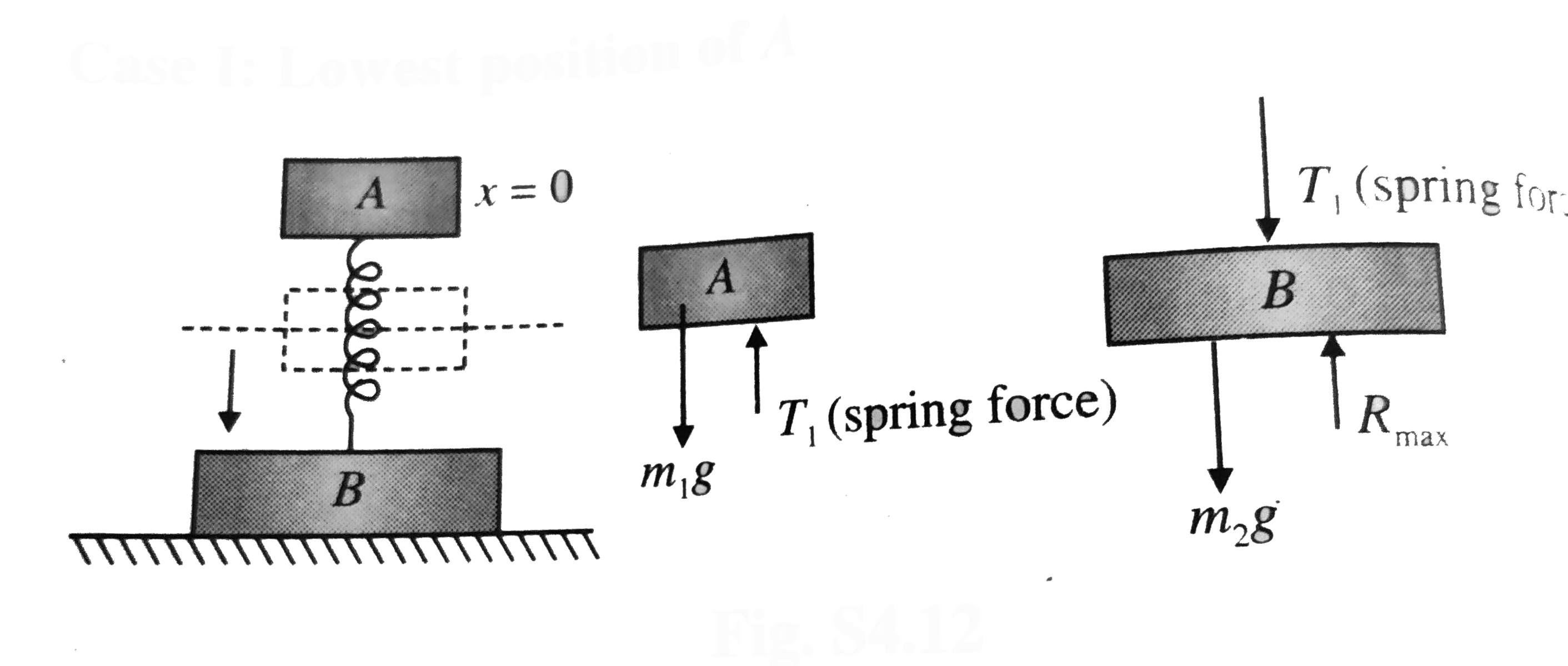
Let T1 be the force in the compressed spring As B is at rest, T1−m2g=Rmax
As acceleration of A is ω2A towards mean position (up).
T1−m1g=m1ω2
Combining, Rmax=(m1+m2)g+m2ω2A
Case II: Topmost position of A

Let T2 be the tension in the elongated spring As B is at rest.
T2+Rmin=m2g
Acceleration of A is ω2A towards mean position (down).
T2−m1g=m1ω2A
Combining, we get Rmin=(m1+m2)g−m1ω2A
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct107videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct35videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.223videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
A body A of mass m1=1kg and a body B of mass m2=4kg are attached to the ends of a spring. The body A performs vertical simple harmonic oscillations of amplitude a=1.6cm and angular frequencyomeg=25rads. Neglecting the mass of the sppring determine the maximum and minimum values of force the system exerts on the surface on which in rests.
[Take g=10m/s2]
 View Solution
View SolutionTwo bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A body A of mass m1 and body B of mass m2 are interconnected by a massless spring as shown. The body A performs free vertical harmonic oscillations with the amplitude A and frequency f. The maximum value of f such that body B does not leave the surface is
 A12π√(m1+m2m2)gAB12π√(m1+m2m1)gAC12π√gAD12π√m2m1.gA
A12π√(m1+m2m2)gAB12π√(m1+m2m1)gAC12π√gAD12π√m2m1.gA - Question 2 - Select One
A body A mass m1 exerts a force on another body B of mass m2 . If the acceleration of B be a2 , then the acceleration (in magnitude) of A is
Am2m1a2Bm1m2a2Cm1m2a2D(m1+m2)a2 - Question 3 - Select One
A particle of mass 1 kg is moving in SHM with an amplitude 0.02 m and a frequency of 60 Hz. The maximum force (in N) acting on the particle is
A188 π2B144 π2C288 π2DNone of the above
A 0.5kg body performs simple harmonic motion with a frequency of 2Hz and an amplitude of 8mm. Find the maximum velocity of the body, its maximum acceleration and the maximum restoring force to which the body is subjected.
View SolutionA block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314s. Find the maximum fore exerted by the spring on the blockl.
View SolutionA body of mass 2m is connected to another body of mass m as shown in figure. The mass 2m performs vertical S.H.M. Then find out the maximum amplitude of 2m such that mass m doesn't lift up from the ground.
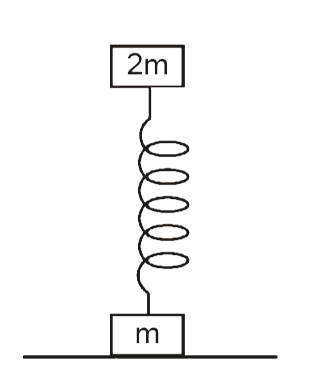 View Solution
View SolutionA body of mass 1 kg suspended by a light vertical spring of spring constant 100 N/m executes SHM. Its angular frequency and frequency are
View SolutionThe scale of a spring balance reading from 0 to 10 kg is 0.25 m long. A body suspended from the balance oscillates vertically with a period of π/10 second. The mass suspended is (neglect the mass of the spring)
View Solution

