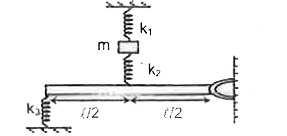
Find out the angular frequency of small oscillation about axis O
The compression in spring (1) = lθ
and the extension in spring (2) = lθ
Net torque opposite to the mean position
=−(2kθ)tl−mgl2sinθ=τnet
θ is small ⇒sinθ=θ
τnet=−Iω2θ=−(2klθ)l−mgl2sinθ−τnet
I=ml23 ⇒ω=√32(4kl+mg)ml
Topper's Solved these Questions
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-A )
8 Videos
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
23 Videos
- SOUND WAVESBOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 3 (Section - B)
14 Videos
Similar Questions
Knowledge Check
A V-shaped glass tube of uniform cross section is kept in a vertical plane as shown. A liquid is poured in the tube. In equilibrium the level of liquid in both limbs of tube are equal. Find the angular frequency of small oscillation of liquid.
 Aπ√2hgsinα.sinβB2π√hgsinα.sinβC2π√h2gsinα.sinβDNone of these
Aπ√2hgsinα.sinβB2π√hgsinα.sinβC2π√h2gsinα.sinβDNone of theseA particle of mass m moves in a one dimensional potential energy U(x)=−ax2+bx4, where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
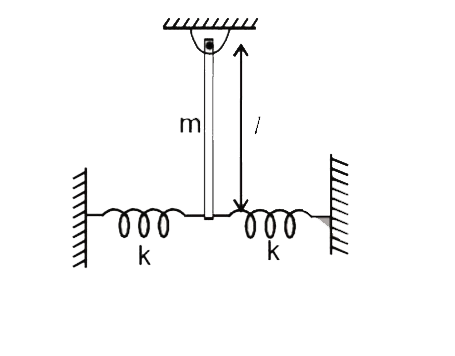
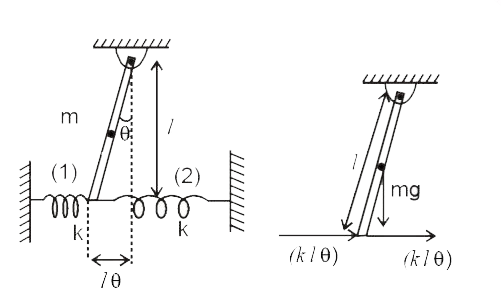
Aπ√a2bB2√amC√2amD√a2mA thin uniform vertical rod of mass m and length l pivoted at point O is shown in Fig. The combined stiffness of the springs is equal to k. The mass of the springs is negligible. The angular frequency of small oscillation is
 A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3l
A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3l
A very light rod of length l pivoted at O is connected with two springs of stiffness k1 & k2 at a distance of a & l from the pivot respectively. A block of mass ma attached with the spring k2 is kept on a smooth horizontal surface. Find the angular frequency of small oscillation of the block m.
_S01_031_Q01.png)
View SolutionA uniform cylinder of mass m and radius R is in equilibrium on an inclined by the action of a light spring of stiffness, gravity and reaction force acting on it .If the angle of inclination of the plane is ϕ , find the angular frequency of small oscillation of the cylinder

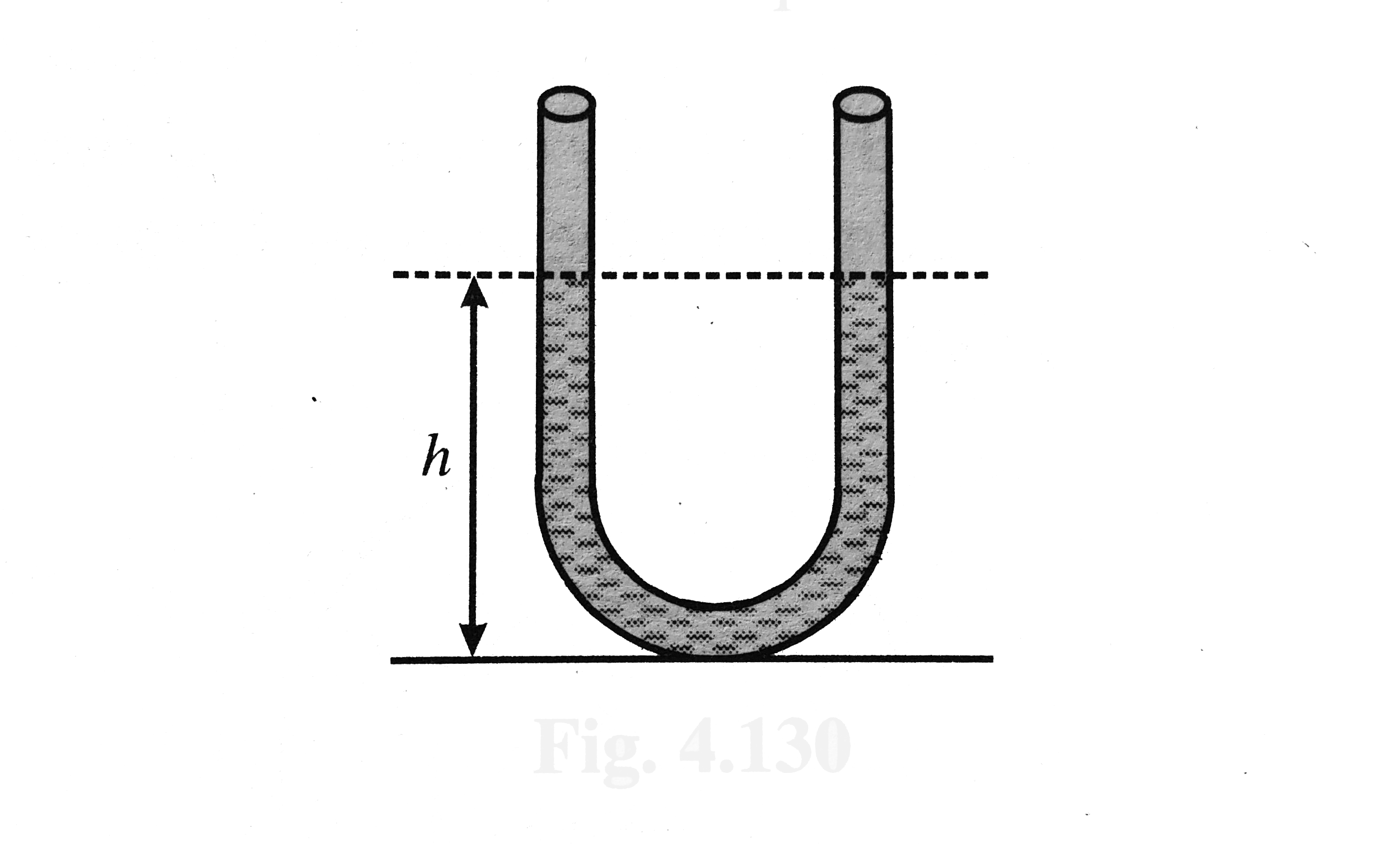
View SolutionConsider a liquid which fills a uniform U - tube uniform U- tube, as shown in figure , up to a height h. Find angular the frequency of small oscillation of th eliquid in the U - tube.
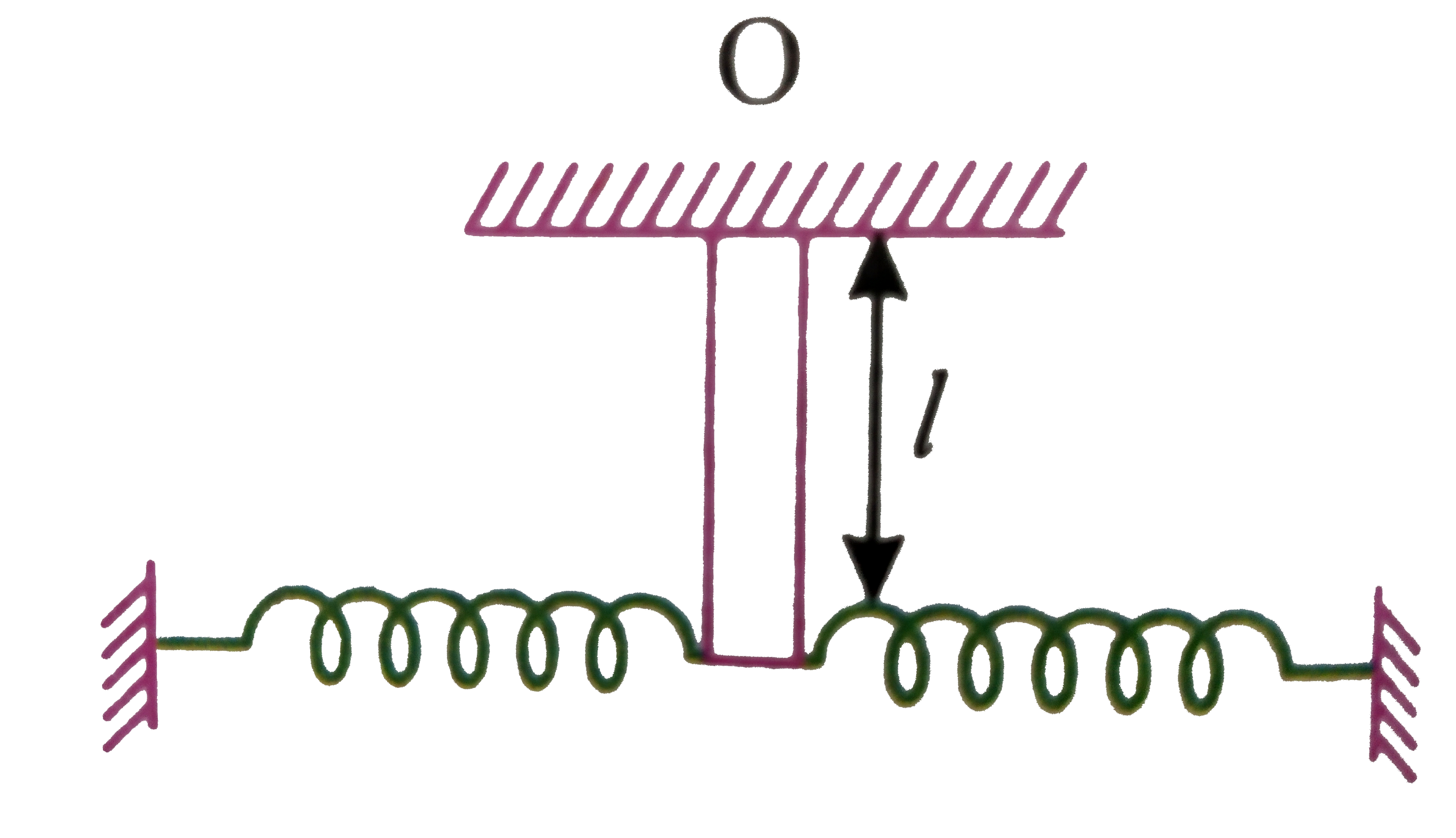
View SolutionIf the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
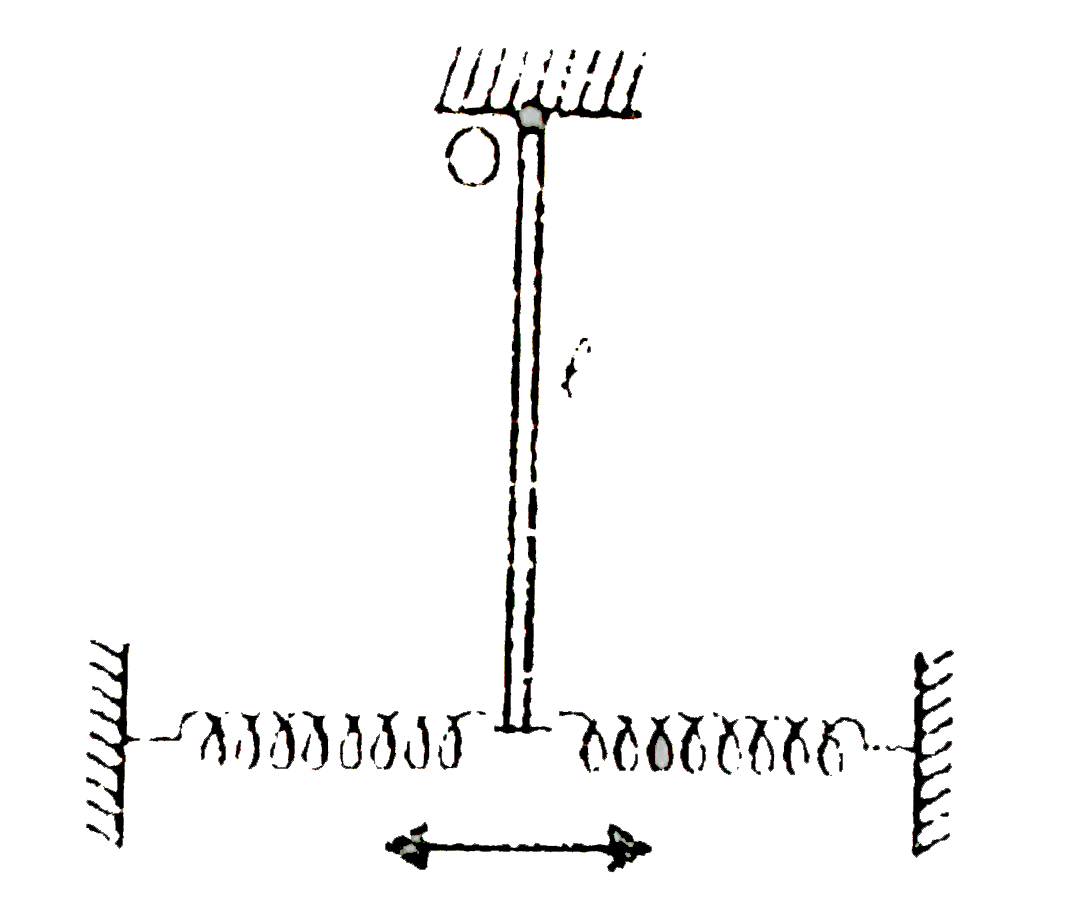
View SolutionIf the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
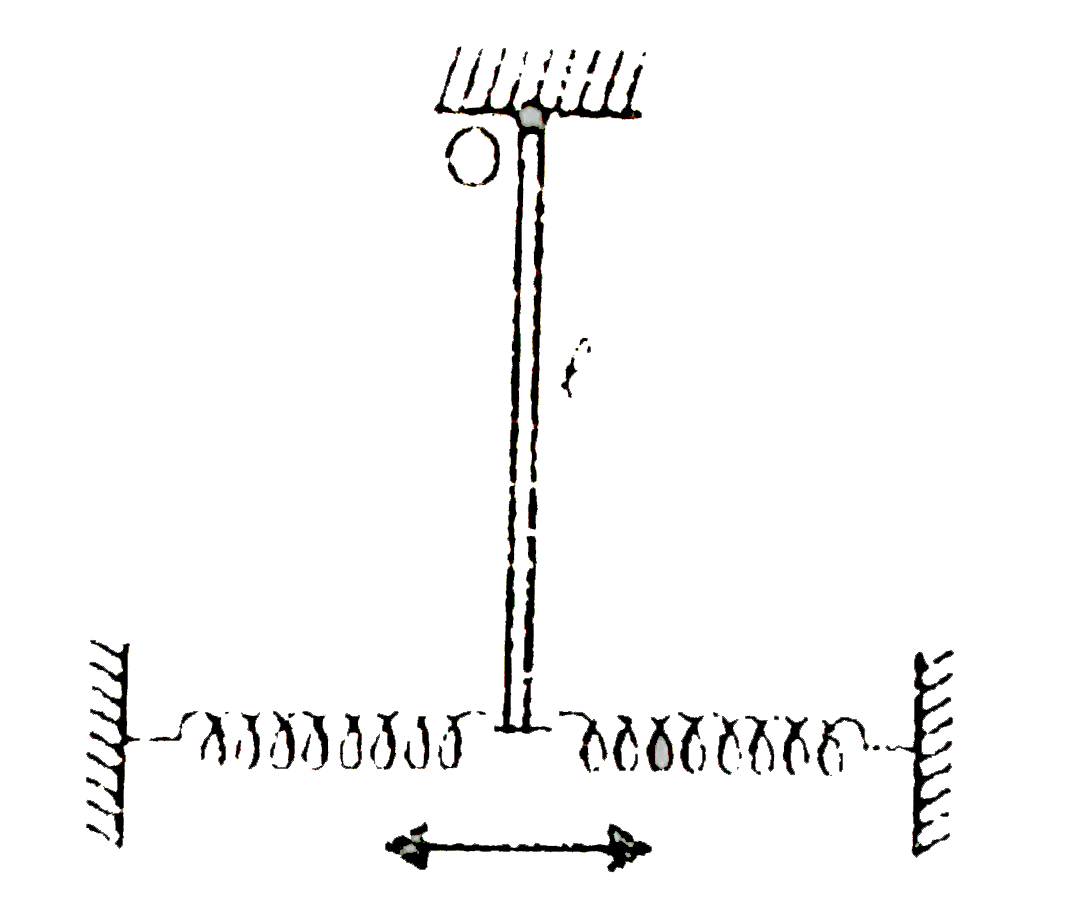
View Solution