A block of mass m moves with a speed v towards the right block which is in equilibrium with a spring attached to rigid wall. If the surface is frictionless and collisions are elastic, the frequency of collisions between the masses will be:
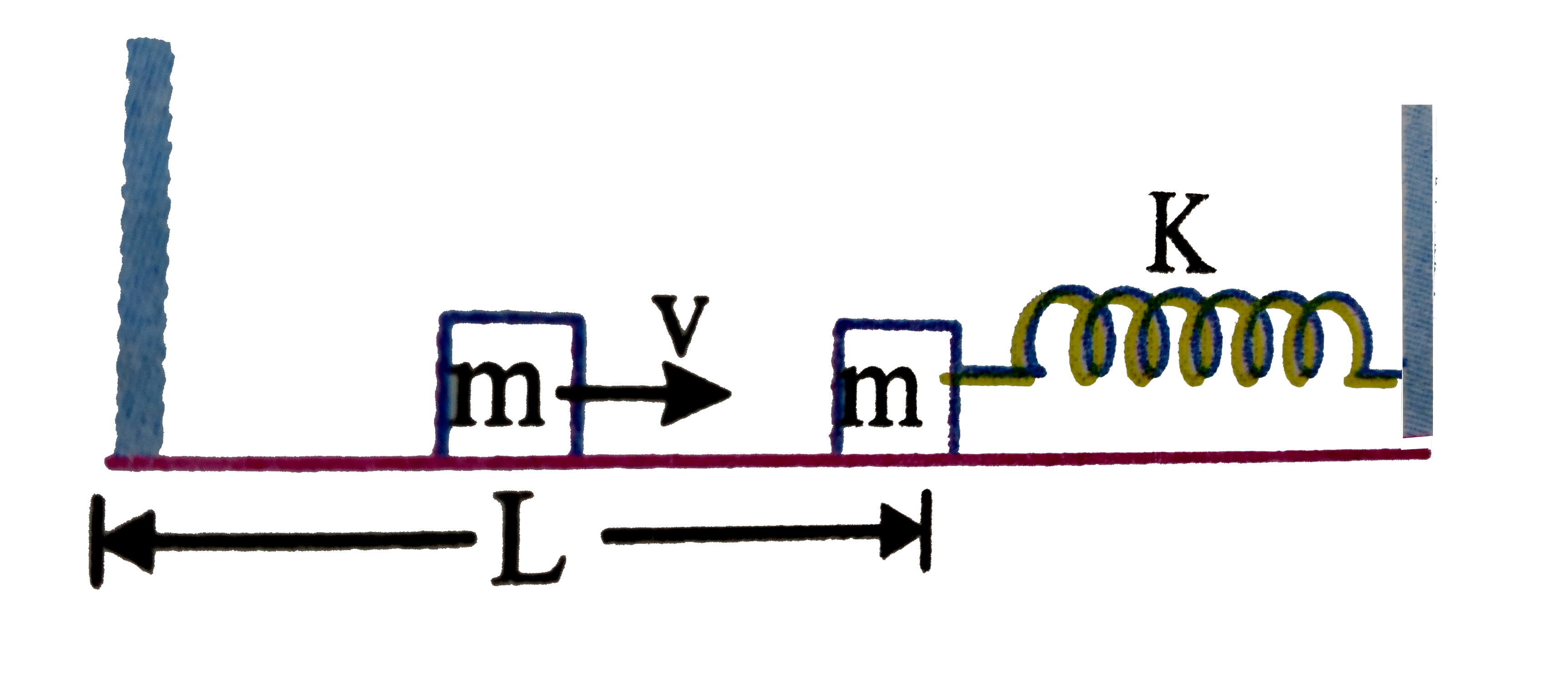
v2L+1π√Km
2[v2L+1π√Km]
1[2LV+π√mK]
2[2LV−π√mK]
The correct Answer is:C
Step by step video & image solution for A block of mass m moves with a speed v towards the right block which is in equilibrium with a spring attached to rigid wall. If the surface is frictionless and collisions are elastic, the frequency of collisions between the masses will be: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-D ) ( Combination of springs)
3 Videos
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-E,F ) ( – Angu lar shm & s implependulum)
10 Videos
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
23 Videos
- SOUND WAVESBOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 3 (Section - B)
14 Videos
Similar Questions
A ball of mass m moving with speed v towards the right strikes a wall moving towards the left with speed u. Find the change in the K.E. of the ball if the collision is elastic.
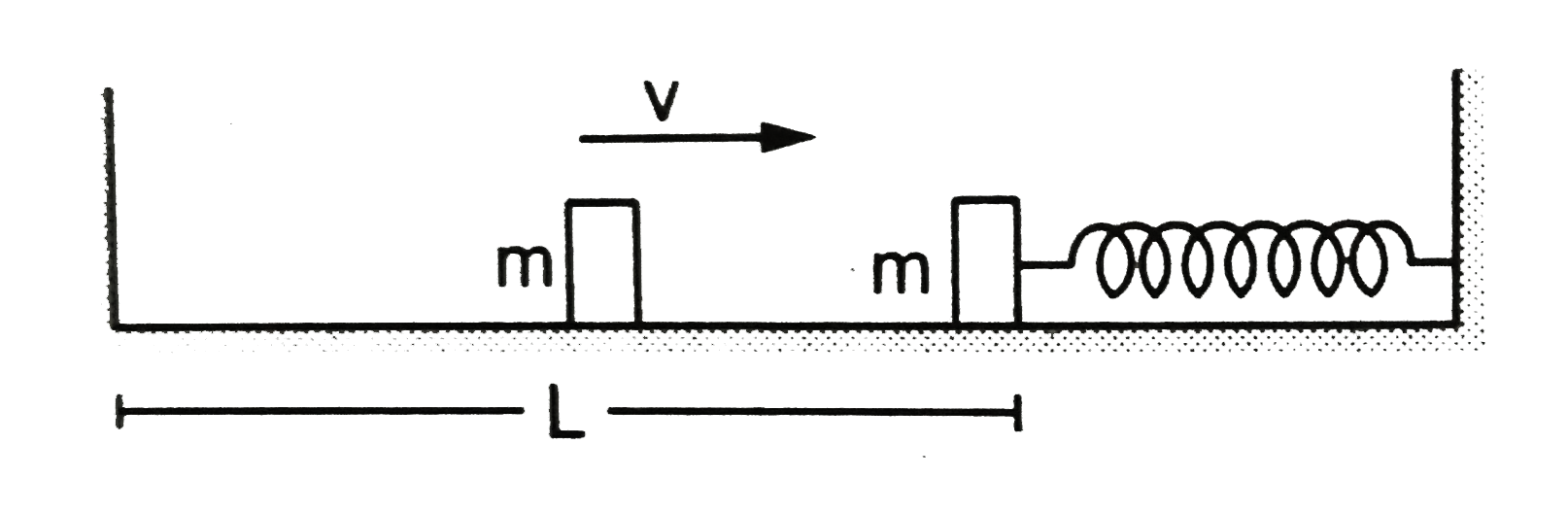
View SolutionThe left block in figure moves at a speed v towards the right block placed in equilibrium. All collilsions to take place are elastic and the surfaces are frictionless. Show that motion of the two blocks are periodic. Find the timepoerid of these periodic motions. Neglect the widths of the blocks.
View Solution
Knowledge Check
The right block in figure moces at a speed V towards the left block placed in equilibrium. All the surfaces are smooth and all the collisions are elastic. Find the time period motion. Neglect the width of the blocks.
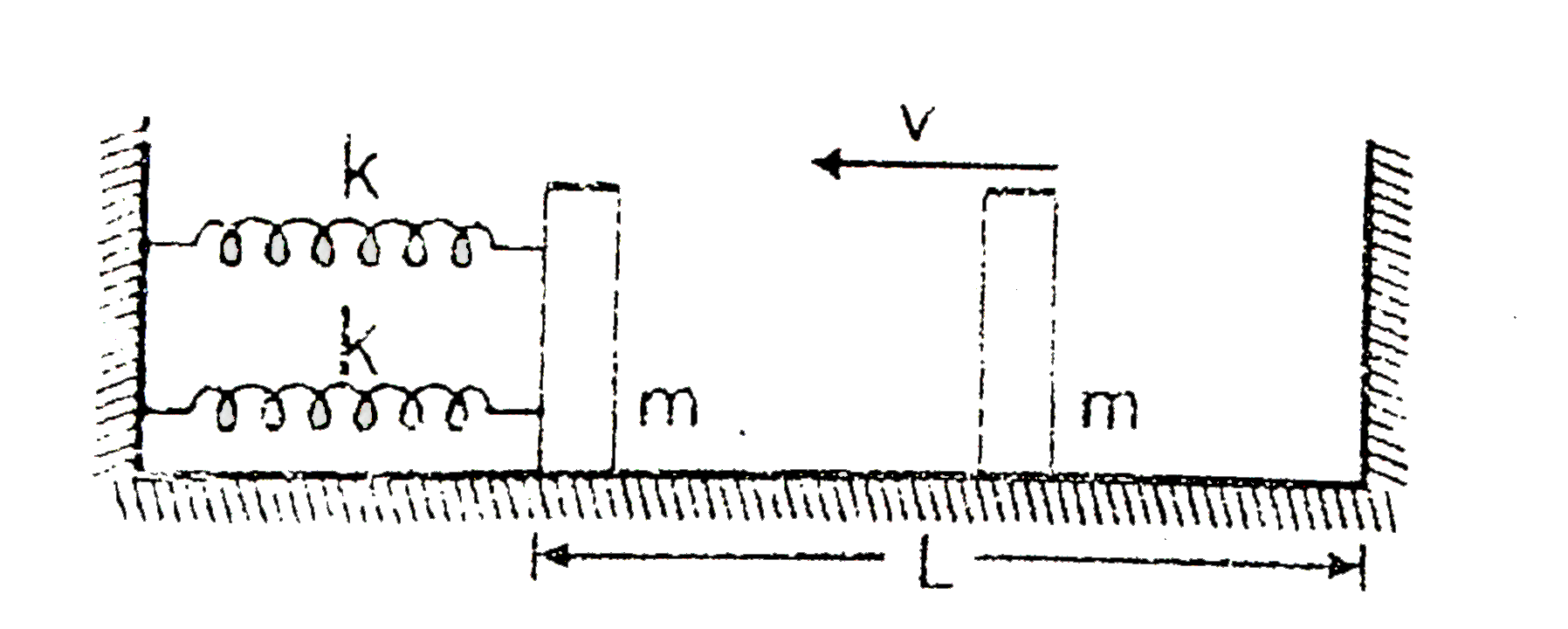 Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+Lv
Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+LvThe right block in figure moces at a speed V towards the left block placed in equilibrium. All the surfaces are smooth and all the collisions are elastic. Find the time period motion. Neglect the width of the blocks.
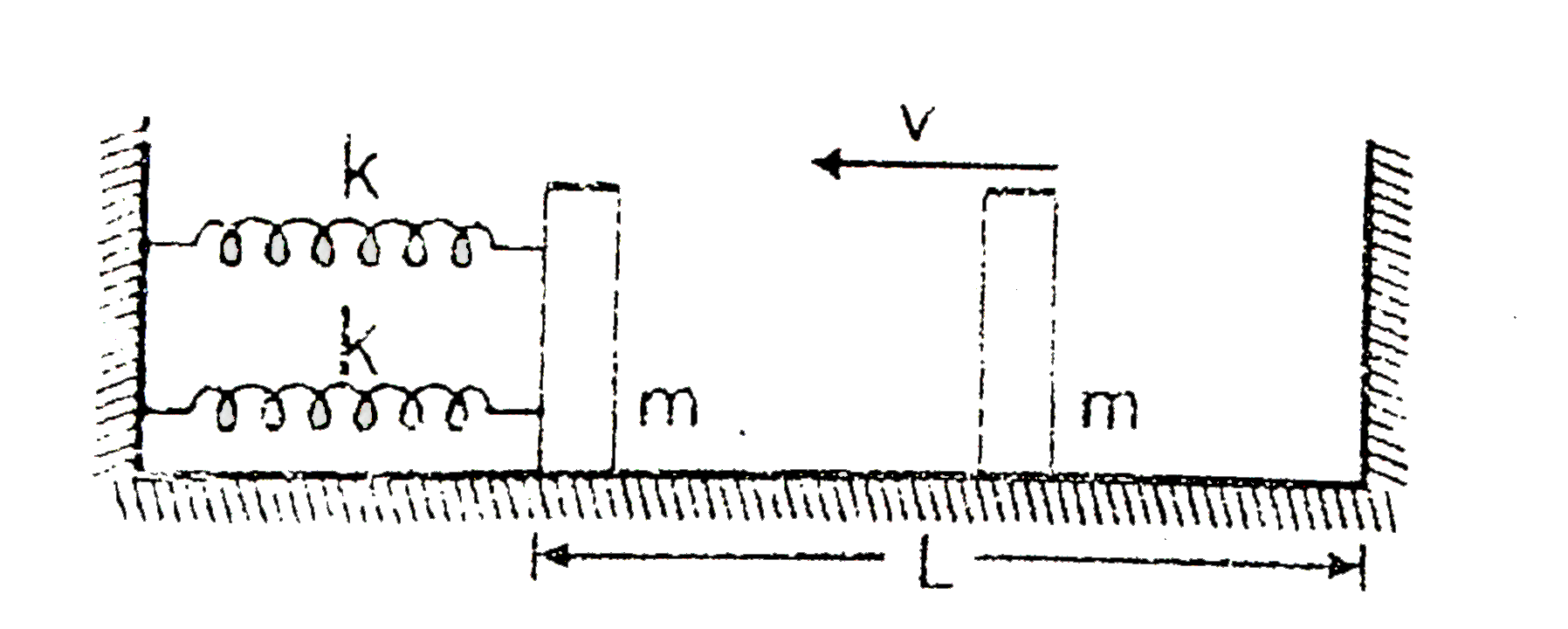 Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+Lv
Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+LvThree blocks are initially placed as shown in the figure. Block A has mass m and initial velocity v to the right. Block B with mass m and block C with mass 4 m are both initially at rest. Neglect friction. All collisions are elastic. The final velocity of block A is
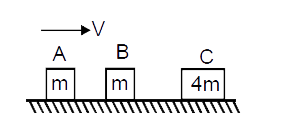 A0.6v to the leftB1.4v to the leftCv to the letD0.4v to the right
A0.6v to the leftB1.4v to the leftCv to the letD0.4v to the right
Infinite blocks each of mass M are placed along a straight line with a distance d between each of them. At t = 0 the leftmost block is given a velocity V towards right. The coefficient of frication between any block and the surface is μ and all collisions are elastic. Let the total number of collisions be N then N is

View SolutionThree blocks are initially placed as shown in the figure. Block A has mass m and initial velocity v to the right. Block B with mass m and block C with mass 4 m are both initially at rest. Neglect friction. All collisions are elastic. The final velocity of block A is

View Solution(i) A block of mass m moving towards right with a velocity V strikes (head on) another block of mass M which is at rest connected to a spring. The coefficient of restitution for collision between the blocks is e = 0.5.
Find the ratio Mm for which the subsequent compression in the spring is maximum. There is not friction.

Ball A collides head on with another identical ball B at rest. Find the coefficient of restitution if ball B has 80% of the total kinetic energy of the system after collision.
View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View Solution
