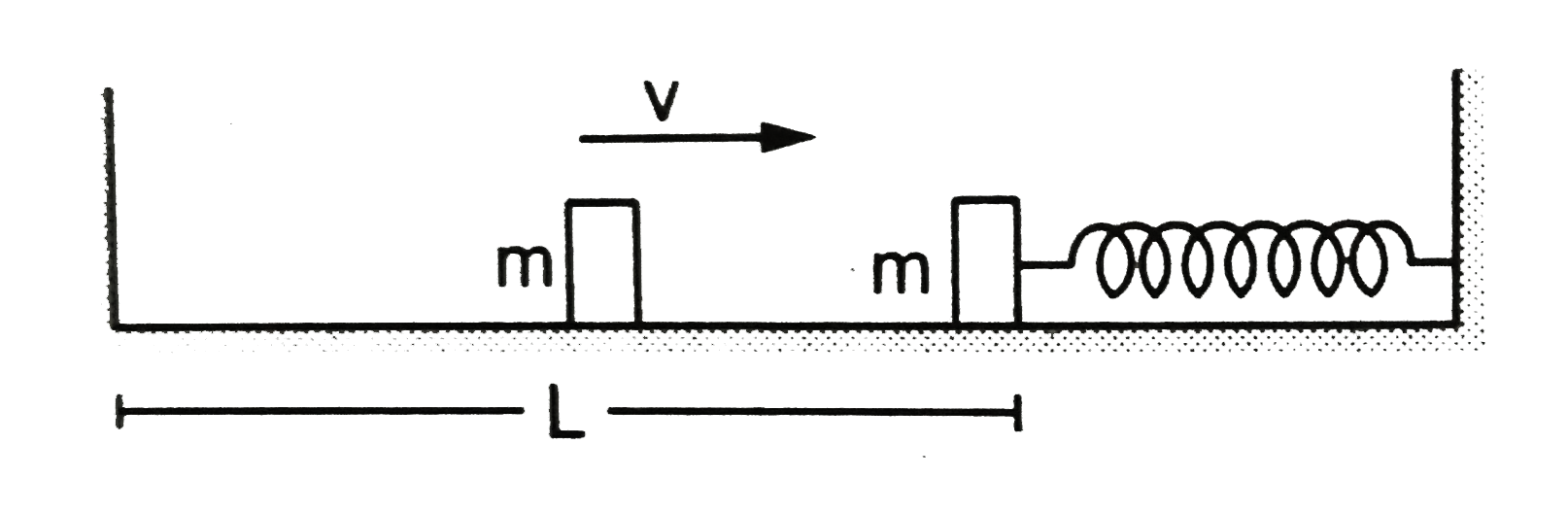
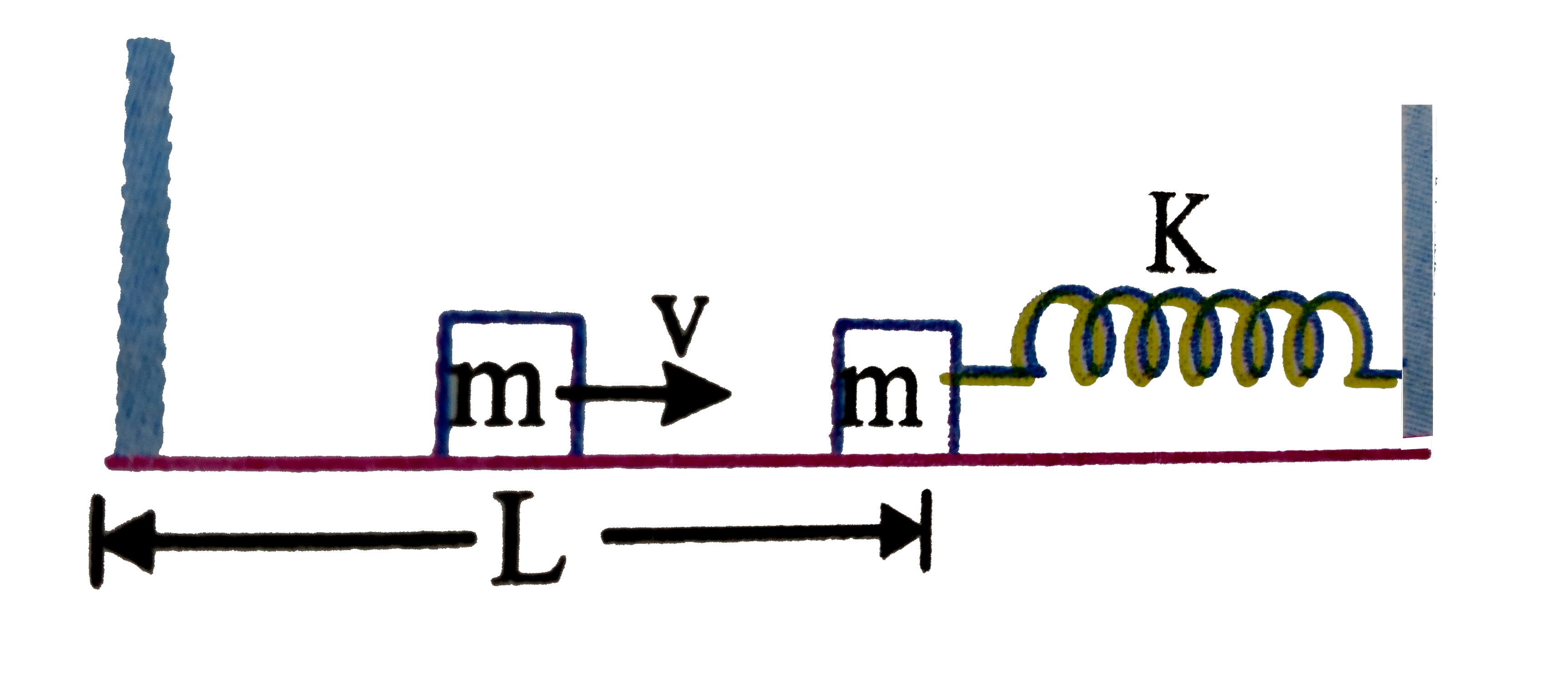
The left block in figure moves at a speed v towards the right block placed in equilibrium. All collilsions to take place are elastic and the surfaces are frictionless. Show that motion of the two blocks are periodic. Find the timepoerid of these periodic motions. Neglect the widths of the blocks.
The correct Answer is:B
When the block A moves with velocity V and collides with the block B, it transfers all energy to the block B. (because it is an elastic collision). The block A will move a distance x against the spring, again the spring, again the block b will return to the origiN/Al point and completes half of the oscillation.
So, the time period of b is
2π√mk2=mk
The block B collides with the block A and comes o rest at that point. The block AS again moves a further distance L to return to its origiN/Al position. The time taken is
LV+LV=2(LV)
So the period of the periodic motion is
2LV+π√(mk)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
The left block in figure collides inelastically with the right block and striks to it. Find the amplitude of the resulting simple harmonic motion
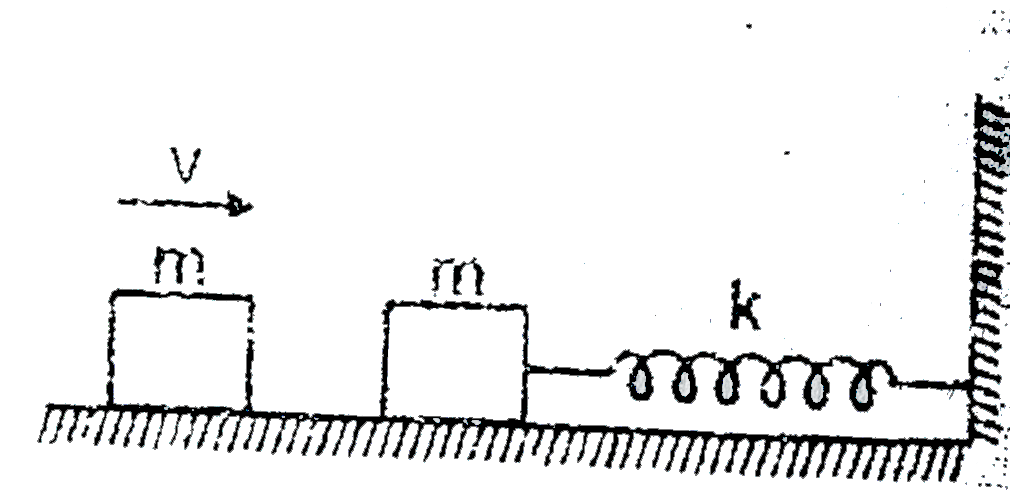
View SolutionThe left block in figure collides inelastically with the right block and sticks to it. Find the amplitude of the resulting simple harmonic motion.

View Solution
Knowledge Check
The right block in figure moces at a speed V towards the left block placed in equilibrium. All the surfaces are smooth and all the collisions are elastic. Find the time period motion. Neglect the width of the blocks.
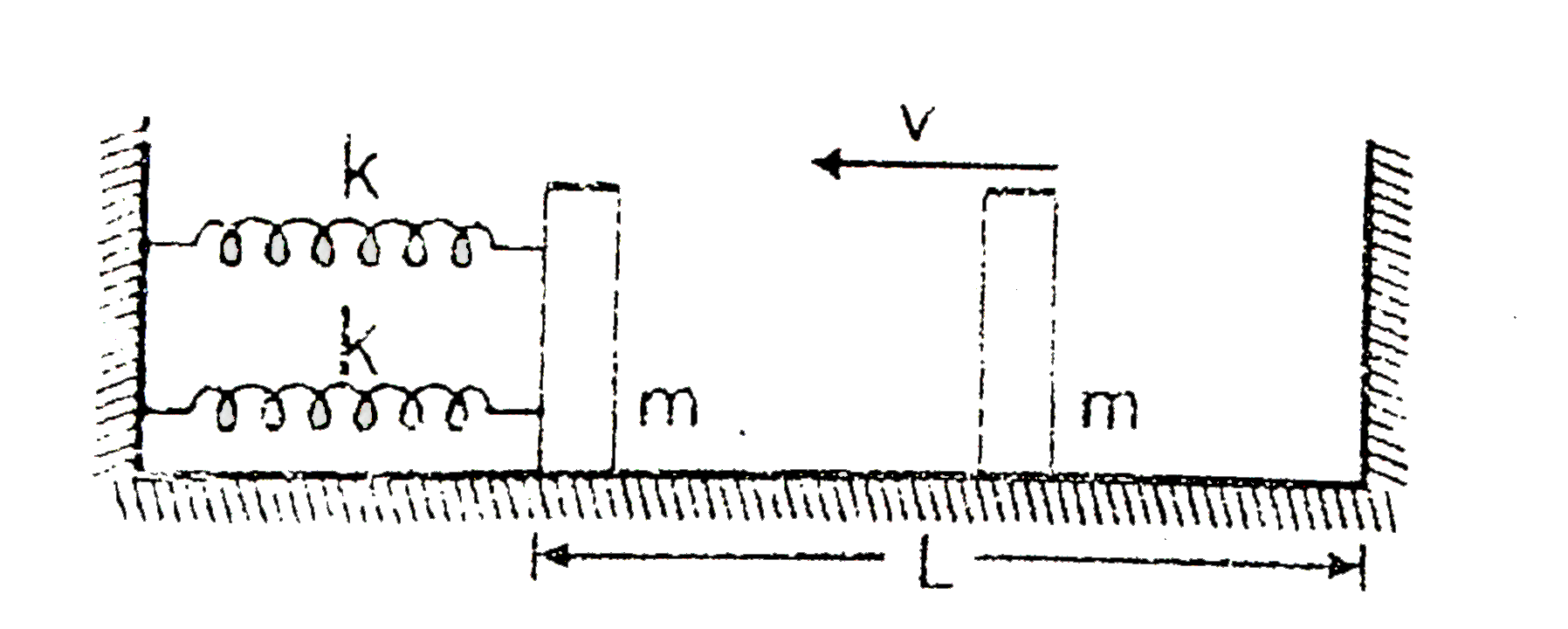 Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+Lv
Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+LvThe right block in figure moces at a speed V towards the left block placed in equilibrium. All the surfaces are smooth and all the collisions are elastic. Find the time period motion. Neglect the width of the blocks.
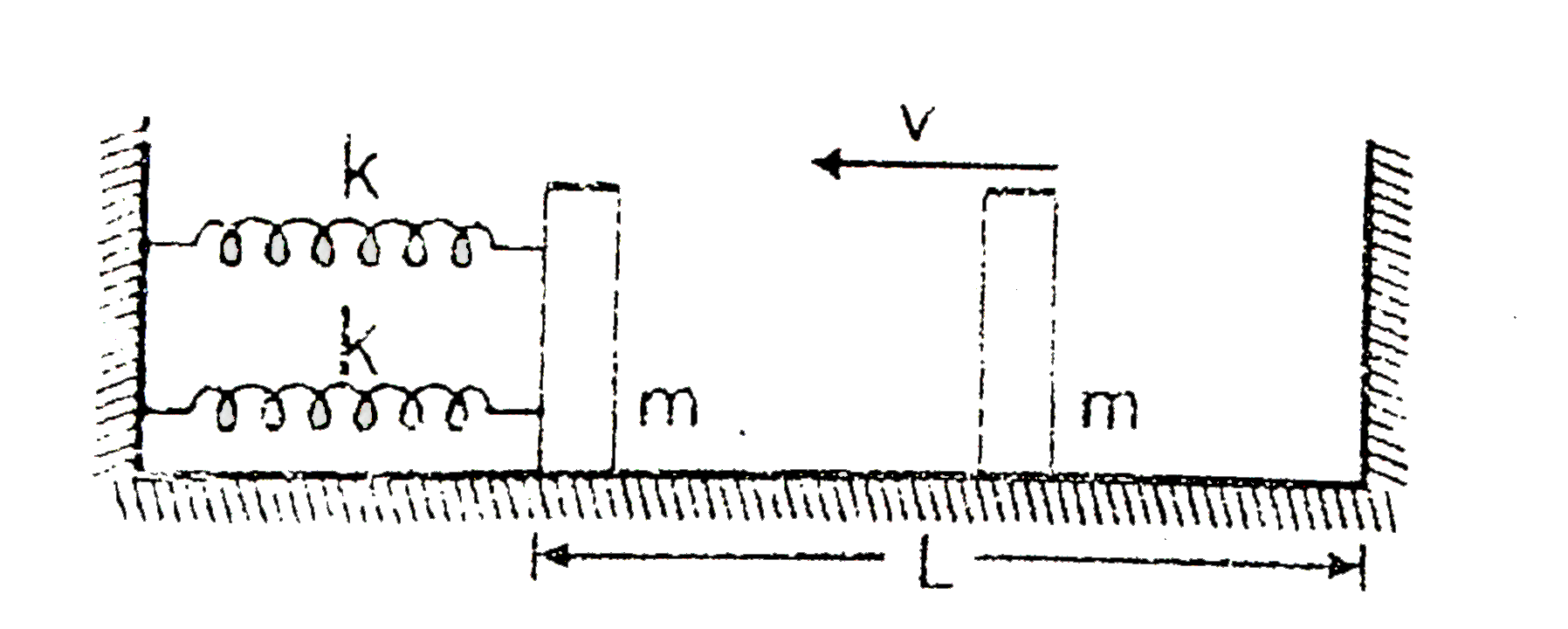 Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+Lv
Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+LvA block of mass m moves with a speed v towards the right block which is in equilibrium with a spring attached to rigid wall. If the surface is frictionless and collisions are elastic, the frequency of collisions between the masses will be:
 Av2L+1π√KmB2[v2L+12π√Km]C2[2Lv+π√mK]Dv2l+1π√mK
Av2L+1π√KmB2[v2L+12π√Km]C2[2Lv+π√mK]Dv2l+1π√mK
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.

View SolutionThe left block in filgure collides inelastically with the right block and sticks to it. Find the amplitude of the resulting simple harmonic motion.
View Solution(a) The right block collides with left block and sticks to it. Find amplitude of the resulting SHM.

(b) The block starts from left wall and moves with constant speed v. All collisions are elastic. Find time period of periodic motion.

View SolutionFigure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.

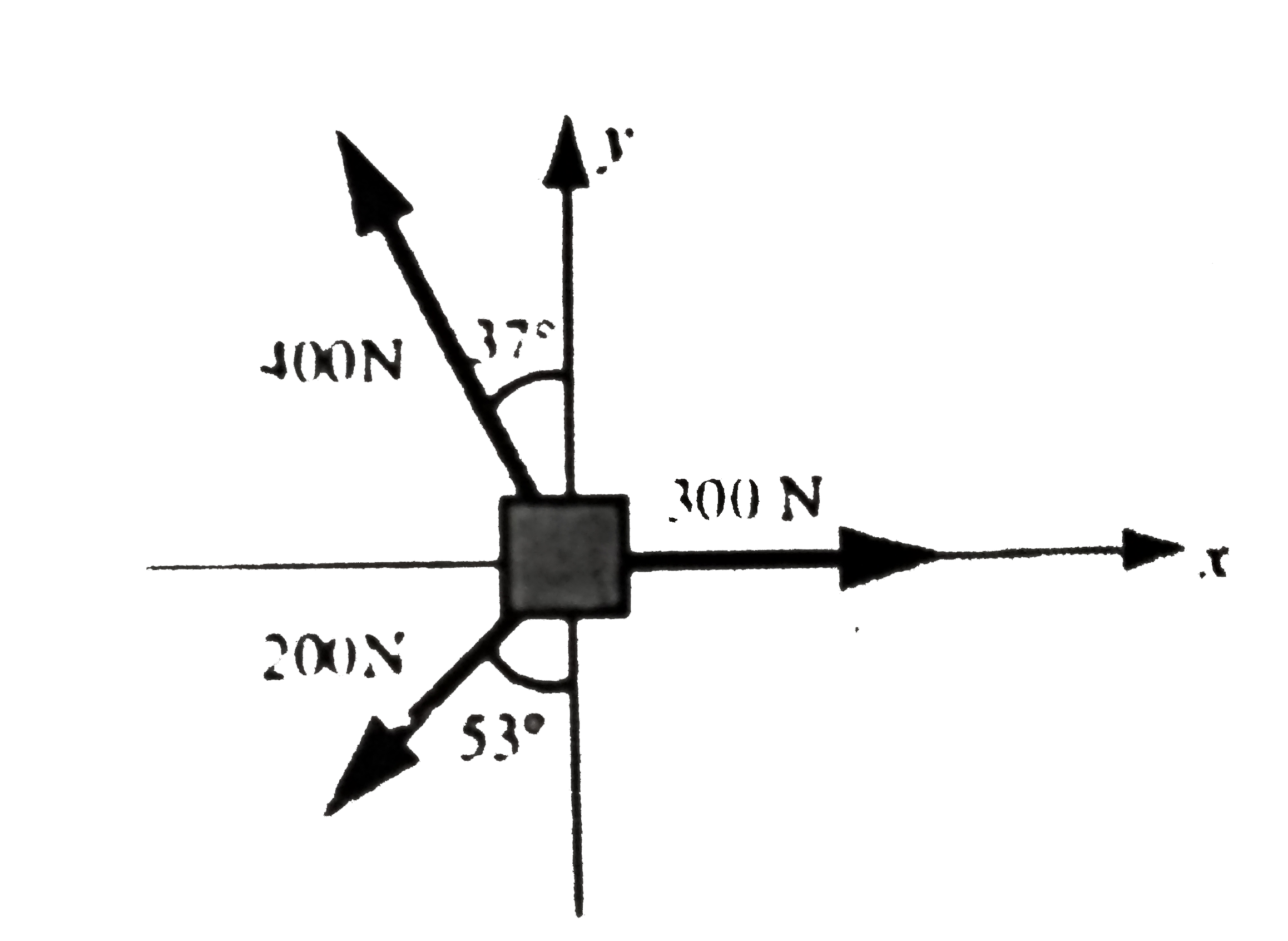
View SolutionA block is placed on a rough horizontal plane. Three horizontalforces are applied on the block as shown in the figure. If the block is in equilibrium, find the friction force acting on the block.
View Solution