A rod of mass m, length l is held horizontal, using a vertical string through its centre. If it is turned a little, the frequency of oscillation will be proportional to- [C-torsional constant of the string]
![A rod of mass m, length l is held horizontal, using a vertical string through its centre. If it is turned a little, the frequency of oscillation will be proportional to- [C-torsional constant of the string]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/MOT_CON_JEE_PHY_C12_E01_037_Q01.png)
√3Cml2
√12Cm
√12Cml2
√m12C
The correct Answer is:C
Step by step video & image solution for A rod of mass m, length l is held horizontal, using a vertical string through its centre. If it is turned a little, the frequency of oscillation will be proportional to- [C-torsional constant of the string] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION - H ) ( Combination of two or more SHM )
4 Videos
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -2 (Leve-I) ( SECTION - A ) ( Equation of SHM, Velocity andAcceleration in SHM, Energy of SHM)
9 Videos
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-E,F ) ( – Angu lar shm & s implependulum)
10 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
23 Videos
- SOUND WAVESBOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 3 (Section - B)
14 Videos
Similar Questions

A uniform rod of mass m and length l is held horizontally by two vertical strings of negligible mass, as shown in the figure.
(a). Immediately after the right string is cut, what is the linear acceleration of the end of the rod?
(b). Of the middle of the rod?
(c). Determine the tension in the left string immediately after the right string is cut.
View SolutionA uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
View Solution
Knowledge Check
If the length of the vibrating string is kept constant, then frequency of the string will be directly proportional to
A√TBTC1TD√1TIf the length of the vibrating string is kept constant , then frequency of the string will be directly proportional to
A√TBTC1TD√1TA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√Tml
A uniform rod of mass m and length L is suspended through two vertical strings of equal lengths fixed at ends. A small object of mass 2m is placed at distance L/4 from the left end. Find the tensions in the two strings.
View SolutionA rod of mass M and length L lying horizontally is free to rotate about a vertical axis through its end. A horizontal force F on the rod at the other end, the force always remains perpendicular to the rod. Find the angular velocity of the rod when it has turned an angle π/2.
View SolutionTwo balls of masses m1=0.5kgandm2=0.3kg are connected by a nonstretchable string and slipped on to a horizontal , light rod. The rod is rotated with ω=110 rpm about a vertical axis passing through its centre. Find the tension of the string and the distance of the masses from the axis of rotation if l=20 cm is the length of the string. Is the equilibrium of the balls stable ?
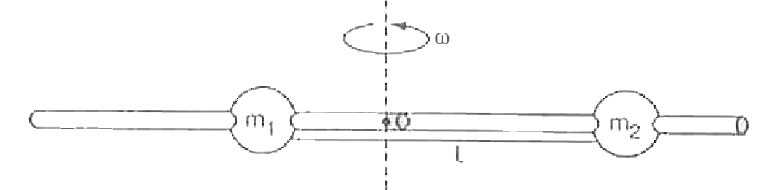
View SolutionA uniform rod of mass m and length 2L on a smooth horizontal surface. A particle of mass m is connected to a string of length L whose other end is connected to the end ‘A’ of the rod. Initially the string is held taut perpendicular to the rod and the particle is given a velocity v0 parallel to the initial position of the rod.
(a) Calculate the acceleration of the centre of the rod immediately after the particle is projected.
(b) The particle strikes the centre of the rod and sticks to it. Calculate the angular speed of the rod after this.

View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View Solution
