A simple pendulum of length l is suspended throught the ceiling of an elevator. Find the time period of small oscilations if the elevator a. is going up with an acceleration a0. b. is going down with an acceleration a0 and c. is moving with a uniform velocity.
(a)2π√la0+g,(b)2π√lg−g0,(c)2π√lg
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -3 (Leve-I) ( SECTION -H ) (Combination of two or more SHM )3videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -3 (Leve-II) ( SECTION -A ) (Equation of SHM, Velocity and Acceleration in SHM, Energy ofSHM)3videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -3 (Leve-I) ( SECTION - E,F ) ( Angu lar shm & s imple pendulum )2videos
SIMPLE HARONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN23videos
SIMPLE HARMONIC MOTION
- BOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 3 (Section - B)14videos
SOUND WAVES
Similar Questions
Two identical rods each of mass m and length L, are tigidly joined and then suspended in a vertical plane so as to oscillate freely about an axis normal to the plane of paper passing through 'S' (point of supension). Find the time period of such small oscillations
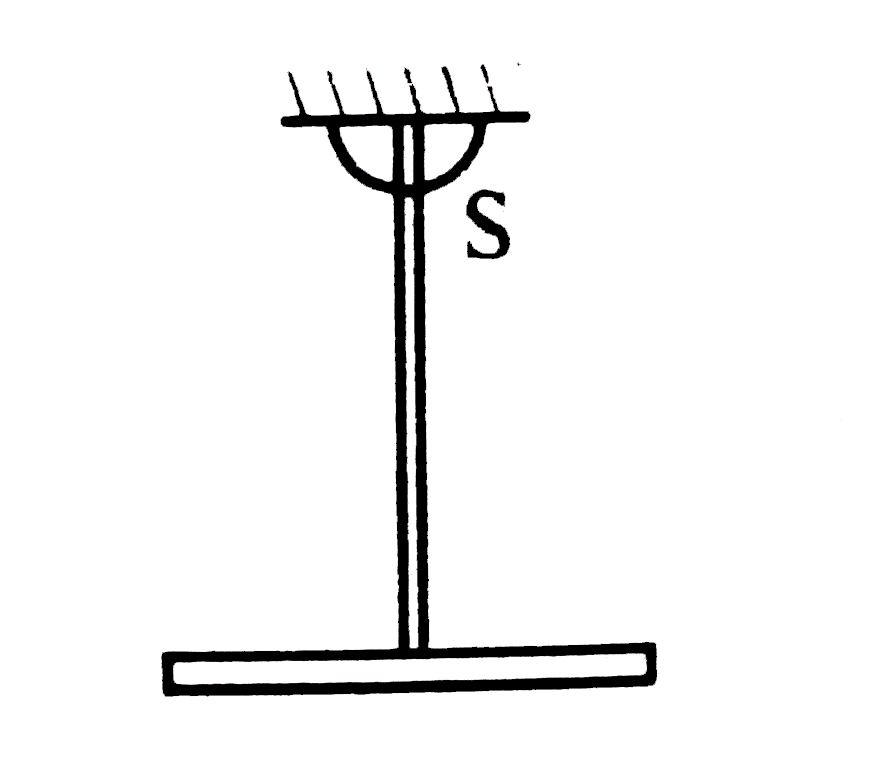 02:34View Solution
02:34View SolutionA point particle of mass 0.1kg is executing SHM with amplitude of 0.1m. When the particle passes through the mean position. Its K.E. is 8×10−3J. Obtain the equation of motion of this particle if the initial phase of oscillation is 45∘.
03:48View SolutionFind the length of seconds pendulum at a place where g=π2m/s2.
05:07View SolutionIf a simple harmonic motion is erpresented by d2xdt2+ax=0,
its time period is.03:10View SolutionAn observer moves towards a stationary source of sound, with a velocity one-fifth of the velocity of sound. What is the percentage increase in the apparent frequency?
07:15View SolutionA simple pendulum is suspnded from the ceilignof a car accelerating uniformly on a horizontal road.If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
01:40View SolutionA simple pendulum of length l is suspended throught the ceiling of an elevator. Find the time period of small oscilations if the elevator a. is going up with an acceleration a0. b. is going down with an acceleration a0 and c. is moving with a uniform velocity.
02:44View SolutionA simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π3 seconds to complete one oscilation. Find the acceleration of the elevator.
02:44View SolutionA simple pendulam 2m long is arranged in an elevator. What will be its time period when the elevator is (a) moving up with uniform velocity 2 m // s, (b) moving up with uniform acceleration 2 ms^(-2) , (c ) going down with uniform acceleration 2 ms^(-2) ?
08:21View Solutionलम्बाई L का एक सरल दोलक एक लिफ्ट की छत से लटकाया गया है। इस दोलक के छोटे आयाम के दोलन का आवर्तकाल निकालें, यदि लिफ्ट (a) ऊपर की और a0 त्वरण से चल रही ही, (b) नीचे की और a0 त्वरण से चल रही हो, (c) एकसमान वेग से चल रही हो।
04:55View SolutionA simple pendulum of length 1 m is freely suspended from the ceiling of an elevator. The time period of small oscillations as the elevator moves up with an acceleration of 2m/s2 is (use g=10m/s2)
06:44View SolutionA simple pendulum of length 1 m is freely suspended from the ceiling of an elevator the time period of small oscollations as the elevator moves up with an acceleration of 2m//s ^2 is ( use g=10 m//s ^2)
02:22View SolutionA simple pendulum of length 1 m is freely suspended from the ceiling of an elevator the time period of small oscollations as the elevator moves up with an acceleration of 2m/s2 is ( use g=10m/s2)
02:44View SolutionA block slides down from top of a smooth inclined plane of elevation theta fixed in an elevator going up with an acceleration a_0 The base of incline has length L. Find the time taken by the block to reach the bottom.
04:59View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an acceleration a0. The base of the incline has a length L. Find the time taken by the particle to reach the bottom.
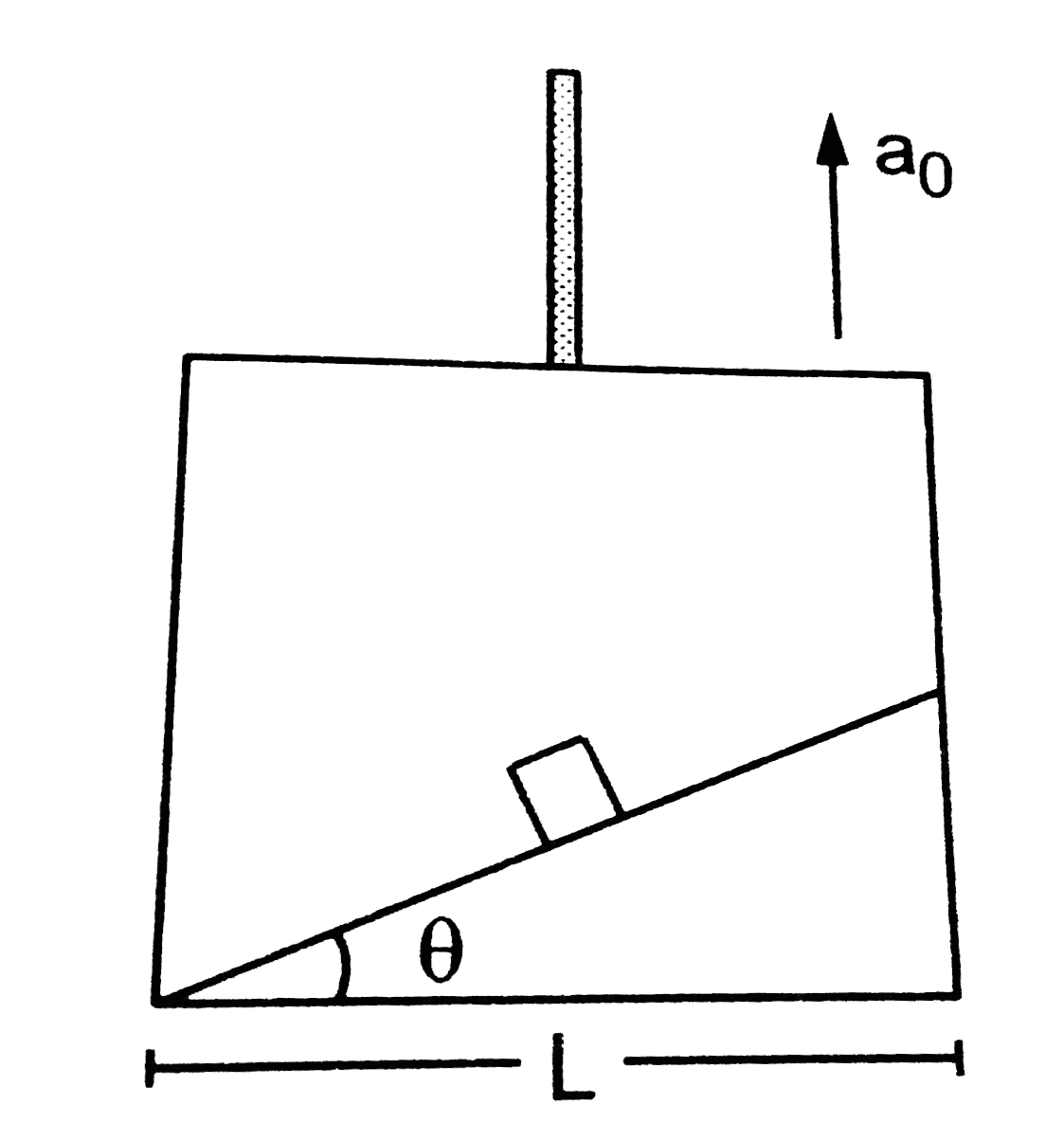 02:50View Solution
02:50View SolutionA simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator a. is going up with an acceleration a0. b. is going down with an acceleration a0 and c. is moving with a uniform velocity.
02:02View Solution

