The figure shows the face and interface temperature of a composite slab containing of four layers of two materials having identical thickness. Under steady state condition, find the value of temperature θ. _E01_247_Q01.png)
The correct Answer is:5∘C
Step by step video & image solution for The figure shows the face and interface temperature of a composite slab containing of four layers of two materials having identical thickness. Under steady state condition, find the value of temperature theta. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -3 (Level - II) Subjective | JEE Advanced11videos
HEAT - 1
- BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -4 (Level - I) Previous Year | JEE Main10videos
HEAT - 1
- BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -2 (Level - II) Multiple Correct | JEE Advanced16videos
HEAT - 1
- BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 4 Section - B Previous Years Problems15videos
GRAVITATION
- BOOK - MOTIONCHAPTER - HEAT TRANSFER & THERMAL EXPANSION EXERCISE - Exercise - 3 Section-B19videos
HEAT TRANSFER & THERMAL EXPANSION
Similar Questions
The figure shows the face and interface temperature of a composite slab containing of four layers of three materials having indentical thickness. Under steady state condition, find the value of temperture θ.
View SolutionThe figure shows the face and interface temperatures of a composite slab consisting of four materials, of identical thickness, through which the heat transfer is steady. Rank the materials according to their thermal conductivities, greatest first.
View Solution
Knowledge Check
- Question 1 - Select One
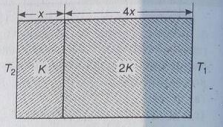
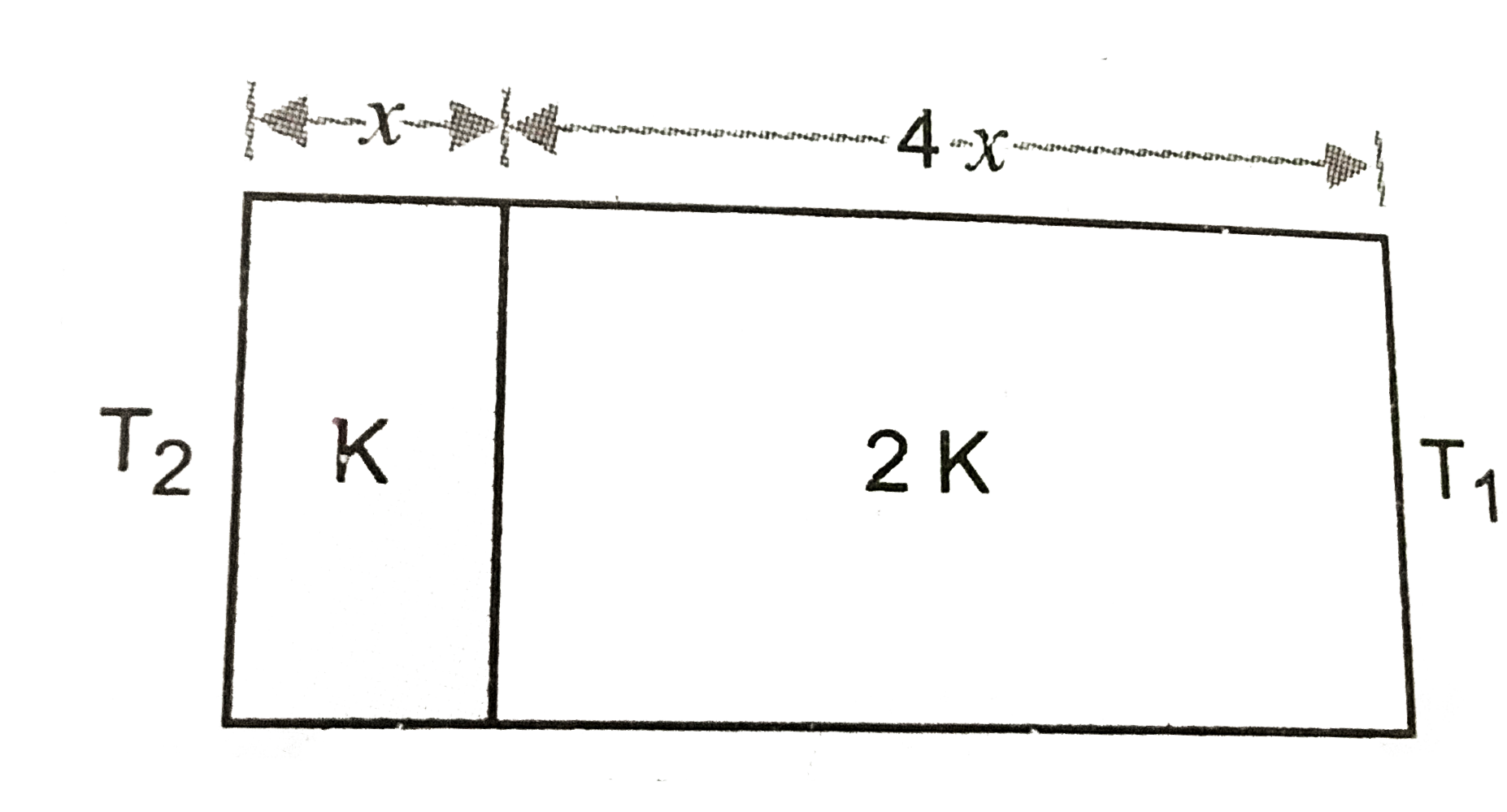
The temperature of the two outer surfaces of a composite slab, consisting of two materails having coefficients of two materails having coefficients of termal conductivity K and 2K and thickness x and 4x, respectively, are T2andT1(T1>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)K2)f, with f equal to
A23B12C1D13 - Question 2 - Select One
The temperature of the two outer surfaces of a composite slab consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab in steady state is (AK(T2−T1)x)f. where, f is equal to
.A1B1/2C2/3D1/3 - Question 3 - Select One
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equals to
A1B1/2C2/3D1/3
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-
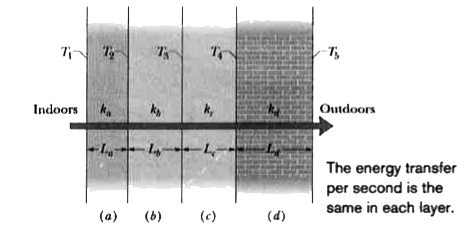
View SolutionFigure shows the cross section of a wall made of white pine of thickness La and brick of thickness Ld==2.0La , sandwiching two layers of unknonw material with identical thicknesses and thermal conductivities. The thermal conductivity of the pine is ka and that of the brick is kd(=5.0ka). The face area A of the wall is unknown. Thermal conduction through the wall has reached the steady state, the only known interface temperatures are T1=25∘C,T2=20∘C, and T5=−10∘C. What is interface temperature T4 ?
View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equals to
View SolutionA hollow and a solid sphere of same material and identical outer surface under identical condition are heated to the same temperature at the same time (both have same e, a):
View Solution