Figure shows the cross section of a wall made of white pine of thickness $L_{a}$ and brick of thickness $L_{d} = = 2.0 L_{a}$ , sandwiching two layers of unknonw material with identical thicknesses and thermal conductivities. The thermal conductivity of the pine is $k_{a}$ and that of the brick is $k_{d} (= 5.0 k_{a})$ . The face area A of the wall is unknown. Thermal conduction through the wall has reached the steady state, the only known interface temperatures are $T_{1} = 25^{\circ} C, T_{2} = 20^{\circ} C$ , and $T_{5} = - 10^{\circ} C$ . What is interface temperature $T_{4}$ ?

Video Solution

Text Solution

Verified by Experts

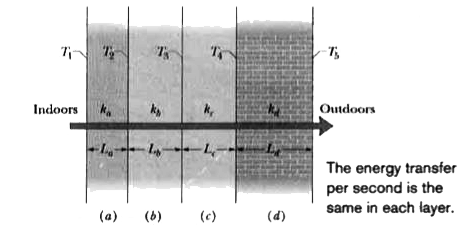
(1) Temperature $T_{4}$ helps determine the rate $P_{d}$ at which energy is conducted through the brick, as given by Equation. However, we lack enough data to solve Equation for $T_{4}$ . (2) Because the conduction is steady, the conduction rate $P_{d}$ through the brick must equal the conduction rate $P_{n}$ through the pine. That gets us going.
Calculations $:$ Frm Equation and Figure, we can write
$p_{a} = k_{a} A \frac{T_{1} - T_{2}}{L_{a}}$ and $P_{d} = k_{d} A \frac{T_{4} - T_{5}}{L_{d}}$
Setting $P_{a} = P_{d}$ and solving for $T_{4}$ yield
$T_{4} = \frac{k_{a} L_{d}}{k_{d} L_{a}} (T_{1} - T_{2}) + T_{5}$
Letting $L_{d} = 2.0 L_{a}$ and $k_{d} = 5.0 k_{a}$ , and inserting th eknown temperature , we find
$T_{4} = \frac{k_{a} (2.0 L_{a})}{(5.0 k_{a}) L_{a}} (25^{\circ} C - 20^{\circ} C) + (- 10^{\circ} C)$
$= - {8.0}^{\circ} C$

Updated on:21/07/2023