Fringe width equal to 1 mm is observed in the interference pattern of biprism experiment. Then the distance of nearest bright fringe from the central bright fringe will be :
1 mm
0.5 mm
2 mm
0.25 mm
The correct Answer is:A
To solve the problem, we need to understand the concept of fringe width in the context of the interference pattern produced by a biprism experiment.
1. Understanding Fringe Width:
The fringe width (β) in an interference pattern is defined as the distance between two consecutive bright or dark fringes. In this case, we are given that the fringe width is 1 mm.
2. Identifying the Central Bright Fringe:
In an interference pattern, the central bright fringe is the one located at the center of the pattern, which is typically designated as the zeroth order fringe (m = 0).
3. Finding the Nearest Bright Fringe:
The nearest bright fringe to the central bright fringe is the first order bright fringe (m = 1). The distance from the central bright fringe to the first order bright fringe is equal to the fringe width (β).
4. Calculating the Distance:
Since the fringe width is given as 1 mm, the distance from the central bright fringe (m = 0) to the nearest bright fringe (m = 1) is simply:
Distance=β=1 mm
5. Conclusion:
Therefore, the distance of the nearest bright fringe from the central bright fringe is 1 mm.
Final Answer:
The distance of the nearest bright fringe from the central bright fringe is 1 mm.
The fringe width (β) in an interference pattern is defined as the distance between two consecutive bright or dark fringes. In this case, we are given that the fringe width is 1 mm.
In an interference pattern, the central bright fringe is the one located at the center of the pattern, which is typically designated as the zeroth order fringe (m = 0).
The nearest bright fringe to the central bright fringe is the first order bright fringe (m = 1). The distance from the central bright fringe to the first order bright fringe is equal to the fringe width (β).
Since the fringe width is given as 1 mm, the distance from the central bright fringe (m = 0) to the nearest bright fringe (m = 1) is simply:
Distance=β=1 mm
Therefore, the distance of the nearest bright fringe from the central bright fringe is 1 mm.
The distance of the nearest bright fringe from the central bright fringe is 1 mm.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 2 (Level - II) (Multiple Correct | JEE Advanced) Section A - Interference Problems + Wavefronts & Hugen’s Principle1videos
WAVE OPTICS
- BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 2 (Level - II) (Multiple Correct | JEE Advanced) Section B - YDSE Experiment1videos
WAVE OPTICS
- BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 2 (Level - I) (Objective Problems | JEE Main) Section B - YDSE Experiment17videos
WAVE OPTICS
- BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - B (Previous Years Problems)7videos
WAVE MOTION
- BOOK - MOTIONCHAPTER - WAVESEXERCISE - EXERCISE -4 (Level -II) (previous year JEE Advanced)10videos
WAVES
Similar Questions
In Young's double slit experiment, the distance between two coherent sources is 1 mm and the distance between the slits and the screen is 1 m. If the 10th dark fringe is at a distance of 4.75 mm from the central bright fringe, calculate
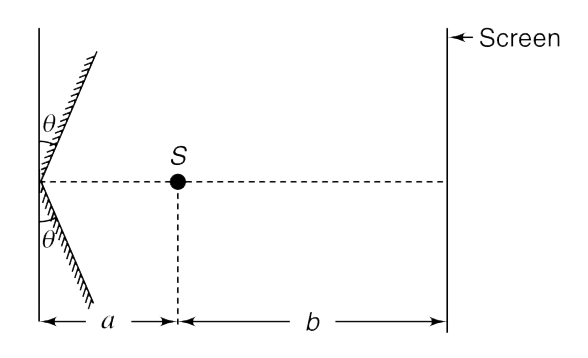
the distance of 5th bright fringe from the central bright fringe.View SolutionTwo plane mirrors, a source S of light, emitting wavelengths ofλ1=4000∘A andλ2=5600∘Aand a screen are arranged as shown in figure. The angle θ shown is 0.05 radian and distance a and b are 1 cm and 38 cm respectively.
(a) Find the fringe width of interference pattern formed on screen by the blue light.
(b) Calculate the distance of first black line from central bright fringe.
(c) Find the distance between two black lines which are nearest to the central bright fringe.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In a Young's double slit experiment, fringe width equal to 1 mm is observed. Then the distance of the nearest bright fringe from the central fringe will be :
A1 mmB0.5mmC2mmDInsufficient data, cannot be determined - Question 2 - Select One
The distance of nth bright fringe from the centre of the interference pattern is
Axn=DdnλBxn=Dd(2n−1)λ2Cxn=DnDxn=nλd - Question 3 - Select One
In a biprism experiment, the distance of the 7th dark band from the central bright band is 2.6 mm. the width of the fringe is
A0.4 mmB0.03 mmC0.8 mmD0.5 mm
The distance of nth bright fringe to the nth dark fringe in Young's experiment is equal to
View SolutionIn Young's double slit experiment, the interference bright fringes are of:
View SolutionA fringe width of a certain interference pattern is β=0.002 cm What is the distance of 5th dark fringe centre?
View SolutionIn a biprism experiment, the fringe width is 0.4mm. The distance between the fourthh dark fringe and the sixth bright fringe is
View SolutionIn an experiment the two slits are 0.5mmapart and the fringes are observed to100cmfrom the plane of theslits ,The distance of the11thbright fringe from the ist bright fringe is 9.72mm.calcualte the wavelength
View Solution

