A capacitor C with a charge Q0 is connected across an inductor through a switch S. If at t=0, the switch is closed, then find the instantaneous charge q on the upper plate of capacitor.
q=2Q0sin(√1LCt+π2)
q=Q02sin(√1LCt+π2)
q=Q0sin(√1LCt+π2)
q=Q0sin(√1LCt−π2)
The correct Answer is:C
Step by step video & image solution for A capacitor C with a charge Q_(0) is connected across an inductor through a switch S. If at t=0, the switch is closed, then find the instantaneous charge q on the upper plate of capacitor. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - MOTIONCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - 2 (LEVEL - II)
5 Videos
- ALTERNATING CURRENTBOOK - MOTIONCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - 3 (LEVEL - I)
11 Videos
- ALTERNATING CURRENTBOOK - MOTIONCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - 1
20 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 4 (Level - II)
49 Videos
- ATOMIC STRUCTURE & X-RAY BOOK - MOTIONCHAPTER - ATOMIC STRUCTURE & X-RAY EXERCISE - Exercise - 2
31 Videos
Similar Questions
The figure shows an RC circuit with a parallel plate capacitor. Before switching on the circuit, plate A of the capacitor has a charge. −Q0 while plate B has no net charge. If at t=0, the switch is closed then after how much time (in seconds) will the net charge on plate A becomes zero? [Given : C=1μF,Q0=1mC,ε=1000VandR=2×1061n3Ω]
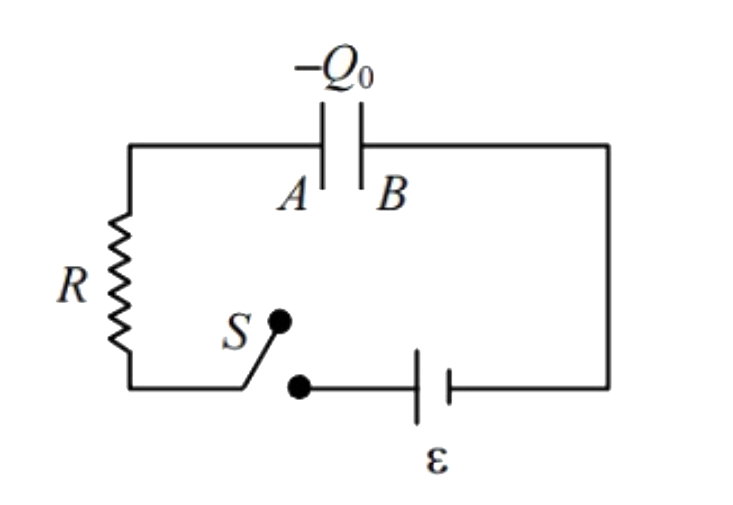
View SolutionIn the circuit shown, a capacitor charged to a potential difference V0 is connected to an uncharged capacitor through a resistor at t=0, by closing the switch. Find current in the circuit as function of time.
.
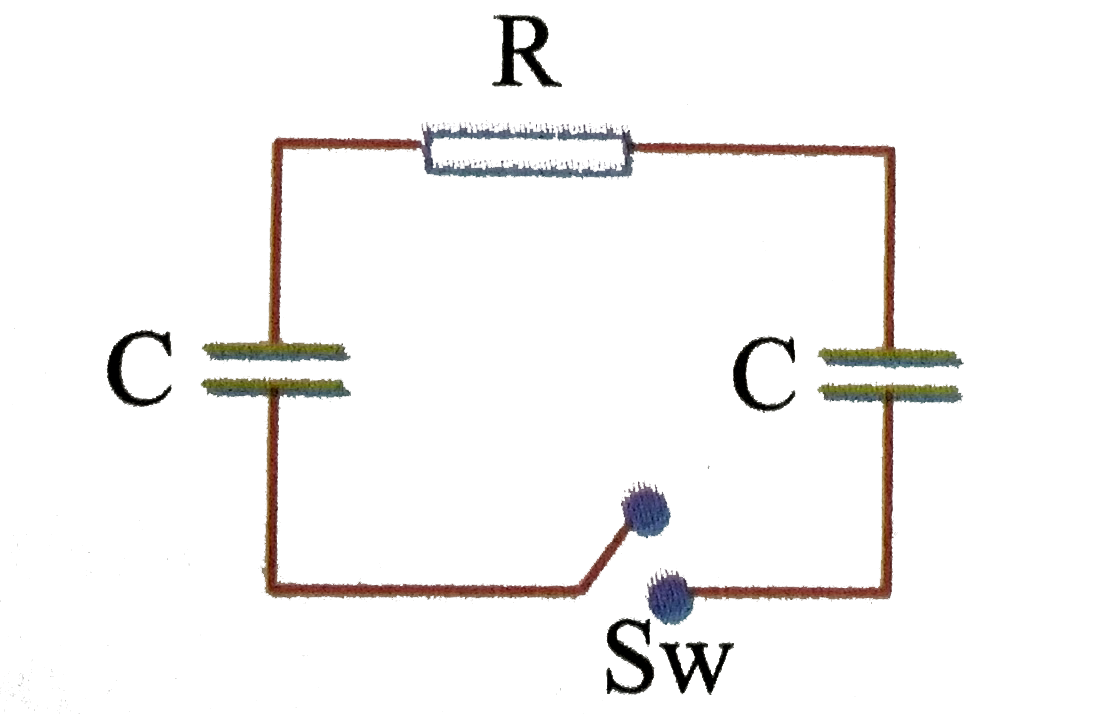View Solution
Knowledge Check
A capacitor is charged to a potential of V0. It is connected with an inductor through a switch S. The switch is closed at time t=0. Which of the following statement(s) is/are correct?
AThe maximum current in the circuit is V0√CLBPotential across capacitor becomes zero for the first time at t=π√LCCEnergy stored in the inductor at time t=π2√LC is 14CV20DMaximum energy stored in the inductor 12CV20In the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is
A(0.37)10μCB(0.37)210μCC(0.63)10μCD(0.63)210μCTwo plates of a charged capacitor are connected to each through a resistance and a switch which is kept open initially. The switch is closed at t= 0. If q is charge on capacitor and I is the current in the circuit at time t then the curves that correctly represent the variation of the change and current with time are:
A
B
C
D
Figure-5.150 shows LC circuit with initial charge on capacitor 200μC. If at t=0 switch is closed, find the first instant when energy stored in inductor becomes one third that of capacitor.
View SolutionFor the circuit shown in figure below, At t = 0, switch is closed, the initial current through resistor and final charge on capacitor are
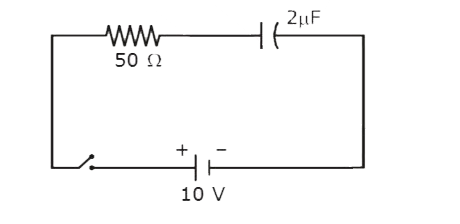
View SolutionIn the circuit shown switches S1 and S2 have been closed for 1sec and S2 remained open.Just after 1 second is over switch S2 is closed and S1,S3 are opened.Find after that instant The charge on the upper plate of the capacitor as function of time taking the instant of switching on of S2 and switching off all time switches to be t=0 is q=x×10−2cos(t+π4).Findout value of x.
View SolutionA capacitor of capacitance C is having a charge Q0. It is connected to a pure inductor of inductance L. The inductor is a solenoid having N turns. Find the magnitude of magnetic flux through each of the N turns in the coil at the instant charge on the capacitor becomes Q02.
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View Solution