(a) Define electric flux. Write its SI units.
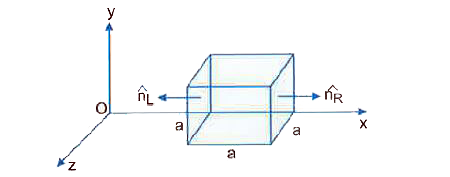
(b) The electric field components due to a charge inside the cube of side 0.1 m are as shown :
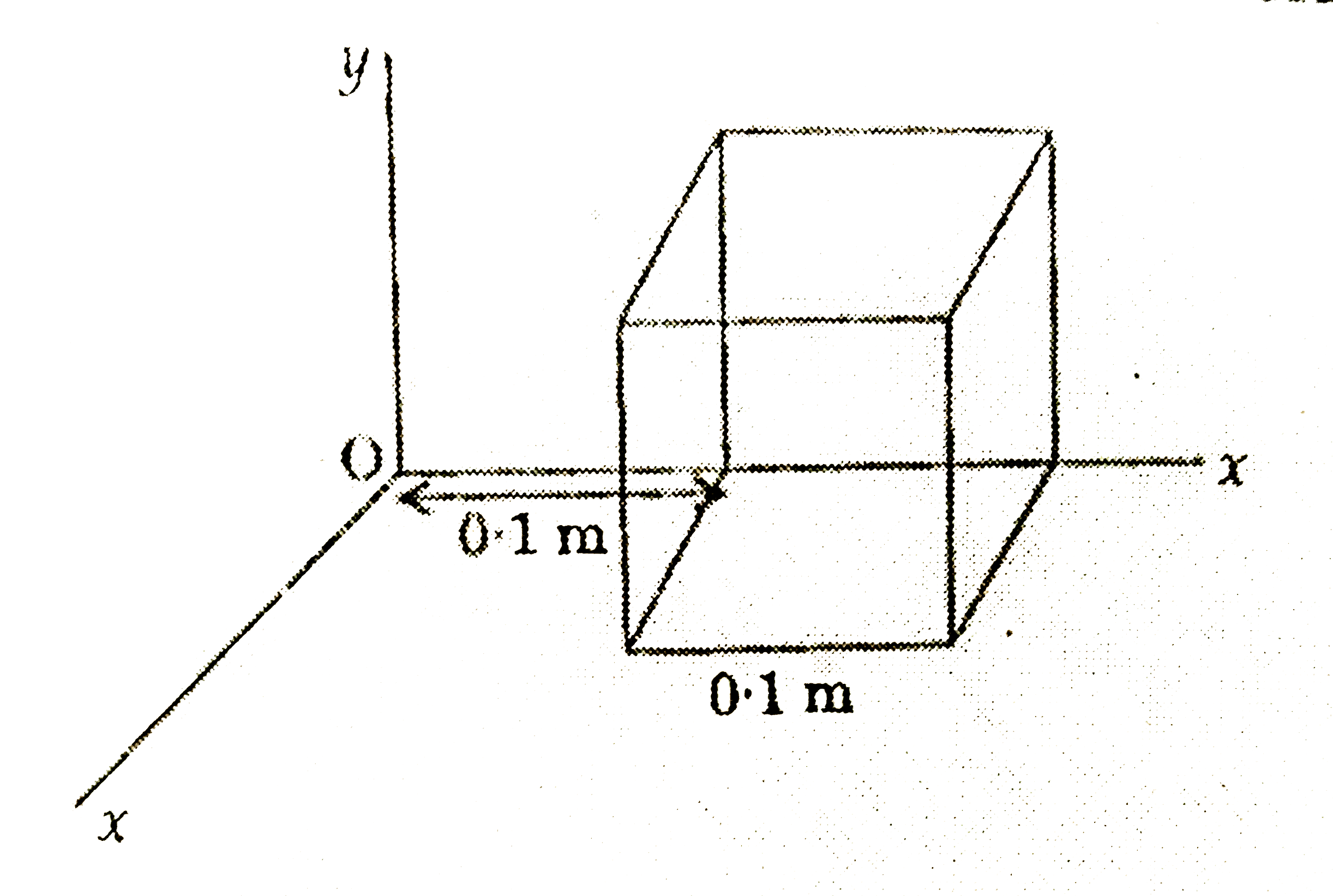
Ex=αx, where α=500N/C−m
Ey=0,Ez=0.
Calculate (i) the flux through the cube, and (ii) the charge inside the cube.
(a) Since the electric field has only an x component. For faces perpendicular to x direction, the angle between E and ΔS is ±π/2. Therefore the flux ϕ=E,ΔS is separately zero for each face of the cube except the two shaded ones. Now th magnitude of the electric the two shaded ones. Now the magnitude of the electric at the left face is
EL=ax3/2=aa1/2
(x=α at the left face)
The magnitude of electric field at the night face is
ER=ax1/2=α(2a)1/2
(x=2a at the right face).
The coresponding fluxes are
ϕL=EL,ΔS=ΔSEL.ˆnL=ELΔScosθ=−ELΔS,sinceθ=180∘=−ELa2
ϕR=ER.ΔS=ERΔScosθ=ERΔS,sinceθ=0∘=ERa2
Net flux through the cube
ϕR=ϕL=ERa2−ELa2=αa3[(2a)1/2−a1/2]
=αa5/2(√2−1)
=800(0.1)5/2(√2−1)
=1.05Nm2C−1
(b) We can use Gauss's law to find th total charge q inside the cube We have ϕ=q/ε0orq=ϕε0 therefore
q=1.05×8.854×10.−12C=9.27×10−12C..
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERTCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE
34 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERTCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
37 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
17 Videos
Similar Questions
Define electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1m area as shown in Ex=αx, where α=500N/Cm,EY=0andEZ=0.
Calculate (i) the flux through the cube , and
(ii) the charges inside the cube.

View SolutionThe electric field componets due to a charge inside the cube of side 0.1m are Ex=αx, where α=500(N/C)m−1,
Ey=0,Ez=0. Calculate the flux through the cube and the charge inside the cube.
View Solution
Knowledge Check
Due to a charge inside the cube, the electric field is: Ex = 600x, Ey = 0, Ez = 0. The charge inside the cube is nearly -
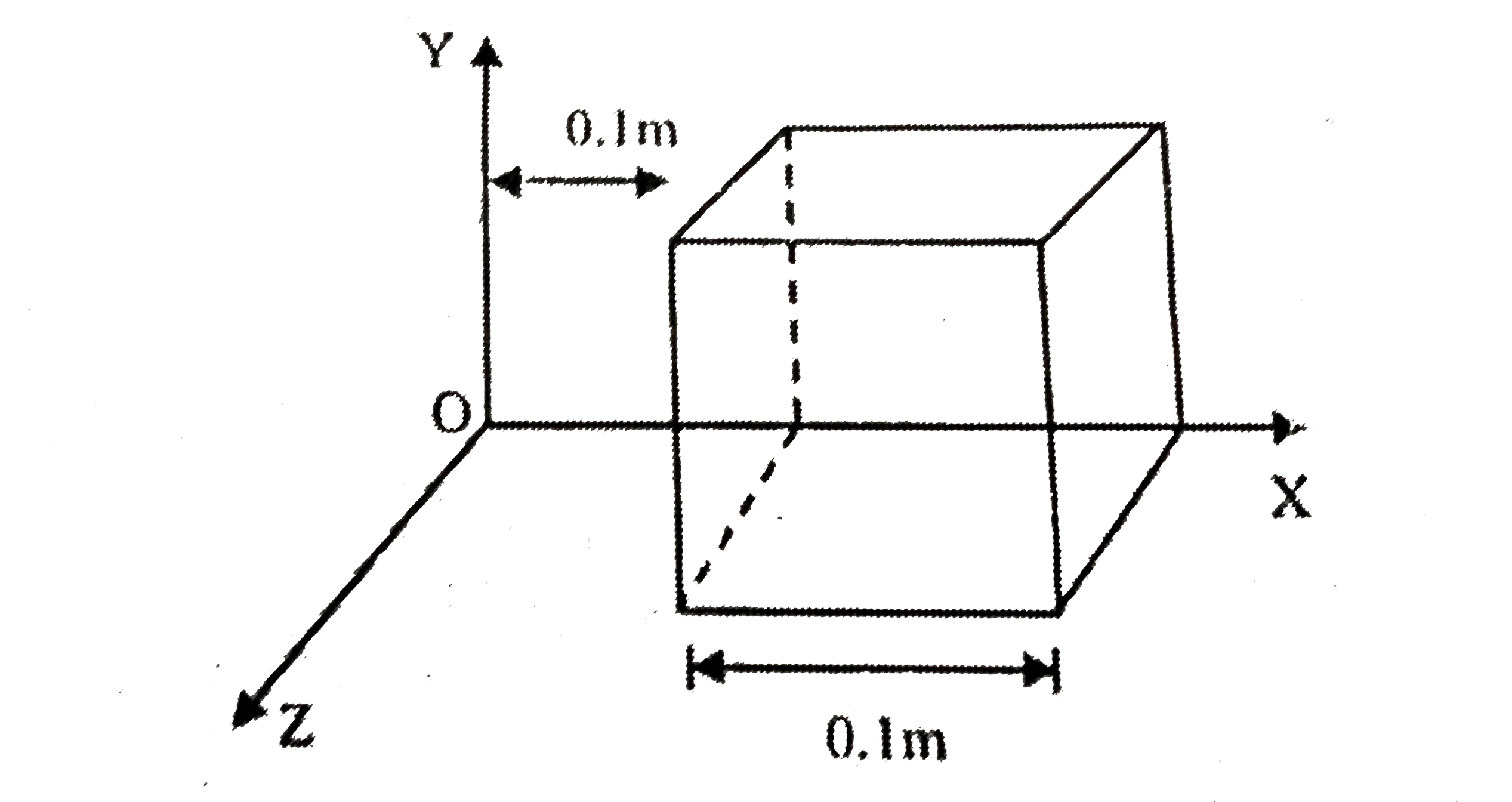 A600μCB60μCC53μCD6μC
A600μCB60μCC53μCD6μCThe electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
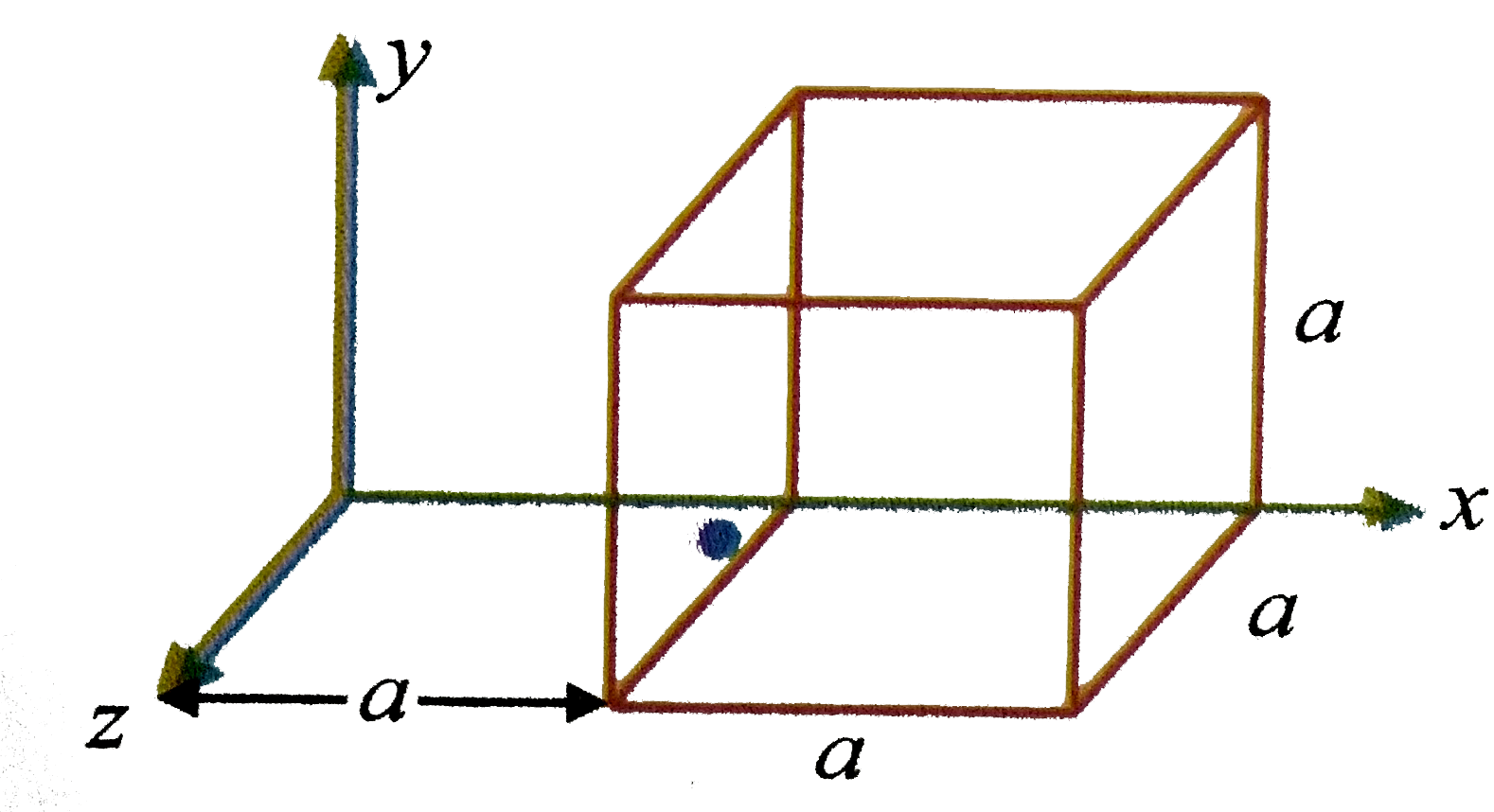 A9.27×10−12CB6×10−12CC2.5×10−12CDZero
A9.27×10−12CB6×10−12CC2.5×10−12CDZero
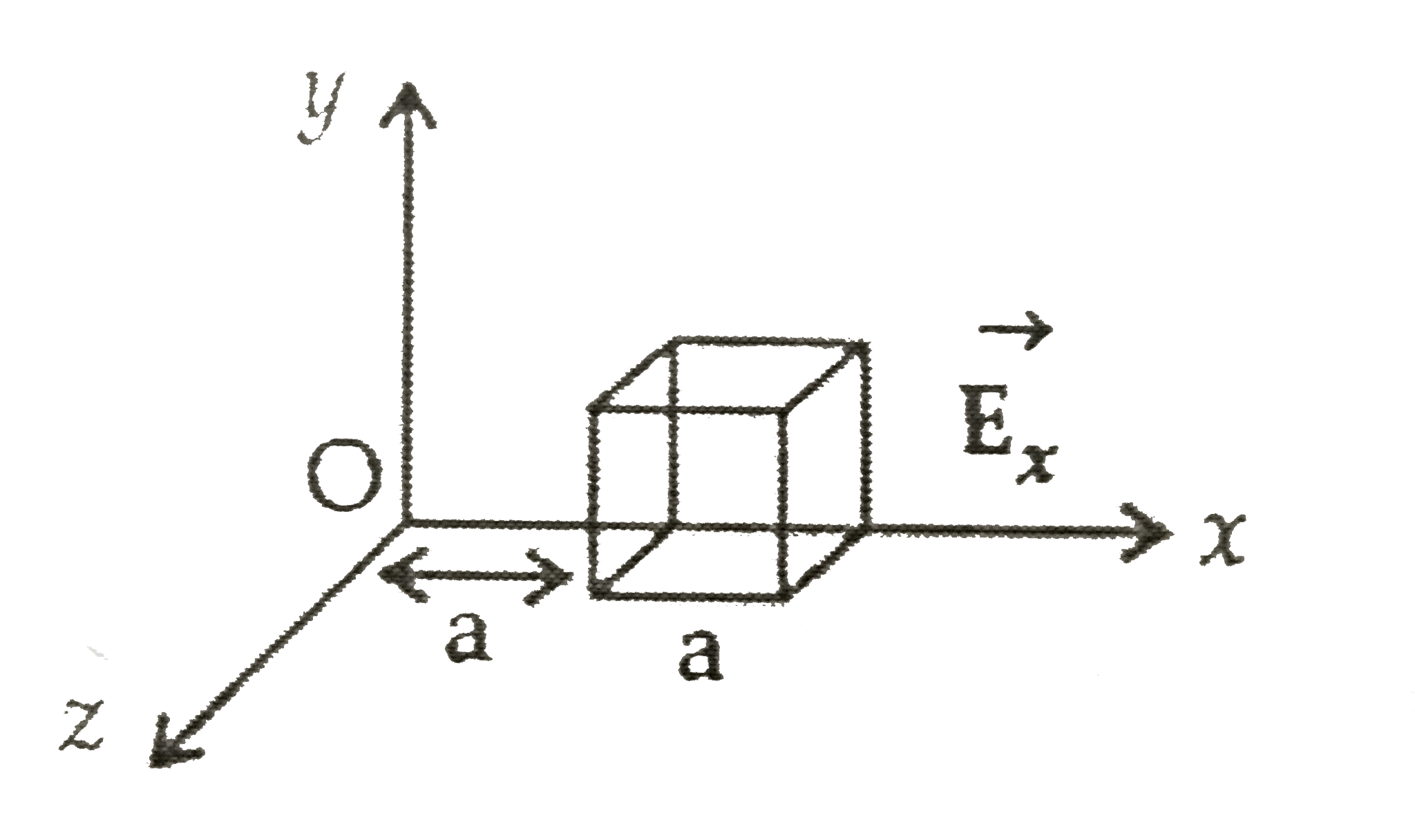
Define electric flux and write its SI unit . The electric field components in the figure shown are : Ex=αx,Ey=0,Ez=0 where α=100NCm.
Calculate the charge within the cube , assuming a = 0.1 m .
View Solution(a) Using Gauss's law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
(b) The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/Cm. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a=0.1m.
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
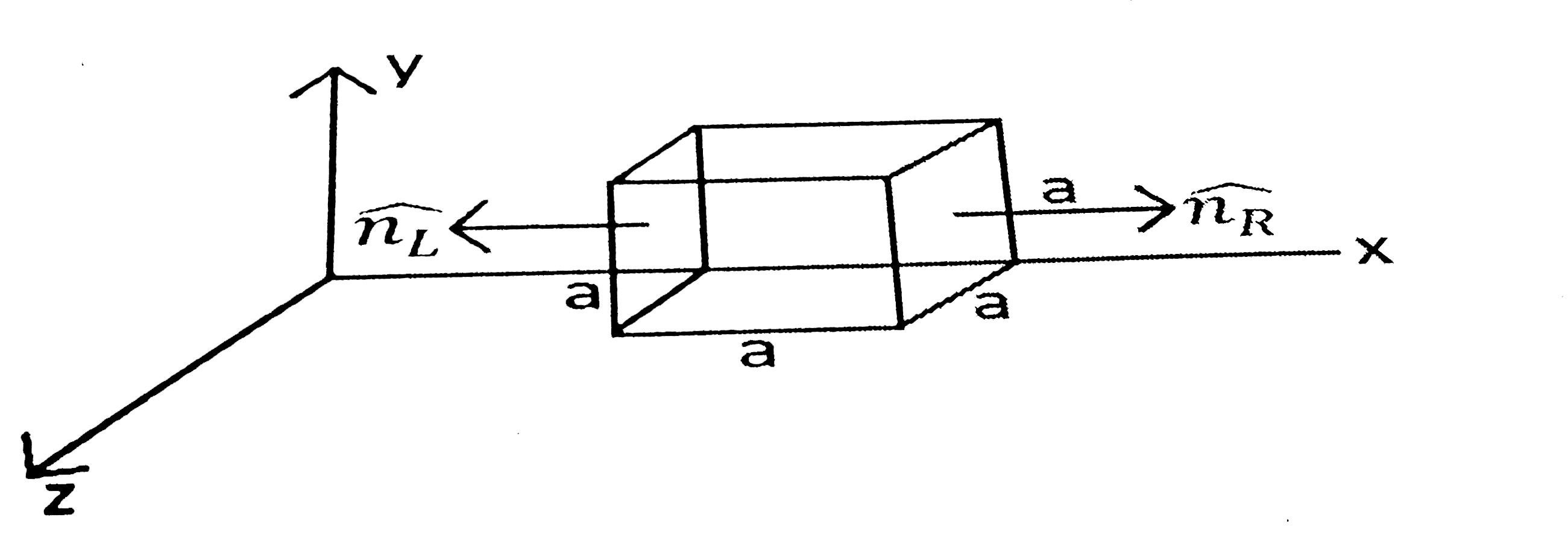
View SolutionGiven the components of an electric field as Ex=αx,Ey=0 and Ez=0, where α is a dimensional constant. Calculate the flux through each face of the cube of side a, as shown in the figure.

View SolutionA non-uniform electric field E=(5xˆi+3ˆj)NC goes through a cube of side length 2.0m oriented as shown. Then,
View Solutioncalculate the electric field at point (5 m, 0) due to a point charge of 1 x 10(-6) C placed at (0,5m).
View Solution
