Find the equations the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2, 2).
To find the equations of the sides of an isosceles right-angled triangle with a given hypotenuse and an opposite vertex, we follow these steps:
1. Identify the Given Information:
- The equation of the hypotenuse is 3x+4y=4.
- The opposite vertex is the point (2,2).
2. Determine the Slope of the Hypotenuse:
- Rewrite the equation of the hypotenuse in slope-intercept form y=mx+b:
4y=−3x+4⟹y=−34x+1
- The slope m of the hypotenuse is −34.
3. Calculate the Slopes of the Other Two Sides:
- Since the triangle is isosceles and right-angled, the angles between the hypotenuse and the other two sides are 45∘.
- The slopes of the two sides can be calculated using the formula for the tangent of the angle between two lines:
tan(45∘)=1=m1−m21+m1m2
- Let m1=−34 (slope of the hypotenuse) and m2 be the slope of one of the sides. Therefore:
1=−34−m21−34m2
4. Solve for m2:
- Cross-multiply:
1−34m2=−34−m2
- Rearranging gives:
1+34=−m2+34m2
74=−m2+34m2
74=−14m2⟹m2=−7
5. Find the Second Slope:
- Now, we can find the second slope using the same method:
1=−34−m′21−34m′2
- This gives us two equations to solve, leading to:
m′2=17
6. Write the Equations of the Lines:
- For the line with slope m2=−7 passing through point (2,2):
y−2=−7(x−2)⟹y=−7x+16⟹7x+y−16=0
- For the line with slope m′2=17 passing through point (2,2):
y−2=17(x−2)⟹7y−14=x−2⟹7y−x−12=0
Final Equations:
1. 7x+y−16=0
2. 7y−x−12=0
- The equation of the hypotenuse is 3x+4y=4.
- The opposite vertex is the point (2,2).
- Rewrite the equation of the hypotenuse in slope-intercept form y=mx+b:
4y=−3x+4⟹y=−34x+1
- The slope m of the hypotenuse is −34.
- Since the triangle is isosceles and right-angled, the angles between the hypotenuse and the other two sides are 45∘.
- The slopes of the two sides can be calculated using the formula for the tangent of the angle between two lines:
tan(45∘)=1=m1−m21+m1m2
- Let m1=−34 (slope of the hypotenuse) and m2 be the slope of one of the sides. Therefore:
1=−34−m21−34m2
- Cross-multiply:
1−34m2=−34−m2
- Rearranging gives:
1+34=−m2+34m2
74=−m2+34m2
74=−14m2⟹m2=−7
- Now, we can find the second slope using the same method:
1=−34−m′21−34m′2
- This gives us two equations to solve, leading to:
m′2=17
- For the line with slope m2=−7 passing through point (2,2):
y−2=−7(x−2)⟹y=−7x+16⟹7x+y−16=0
- For the line with slope m′2=17 passing through point (2,2):
y−2=17(x−2)⟹7y−14=x−2⟹7y−x−12=0
1. 7x+y−16=0
2. 7y−x−12=0
Topper's Solved these Questions
Similar Questions
Find the equations to the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2,2).
View SolutionA side of an isosceles right angled triangle is x. Find its hypotenuse.
View SolutionA side of an isosceles right angled triangle is x. Find its hypotensuse.
View SolutionThe area of an isosceles right - angled triangle is 72 cm2 .Find its hypotenuse .
View SolutionFind the equation of the legs of a right isosceles triangle if the equation of its hypotenuse is x−2y−3=0 and the vertex of the right angle is at the point (1,6),
View SolutionA right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as
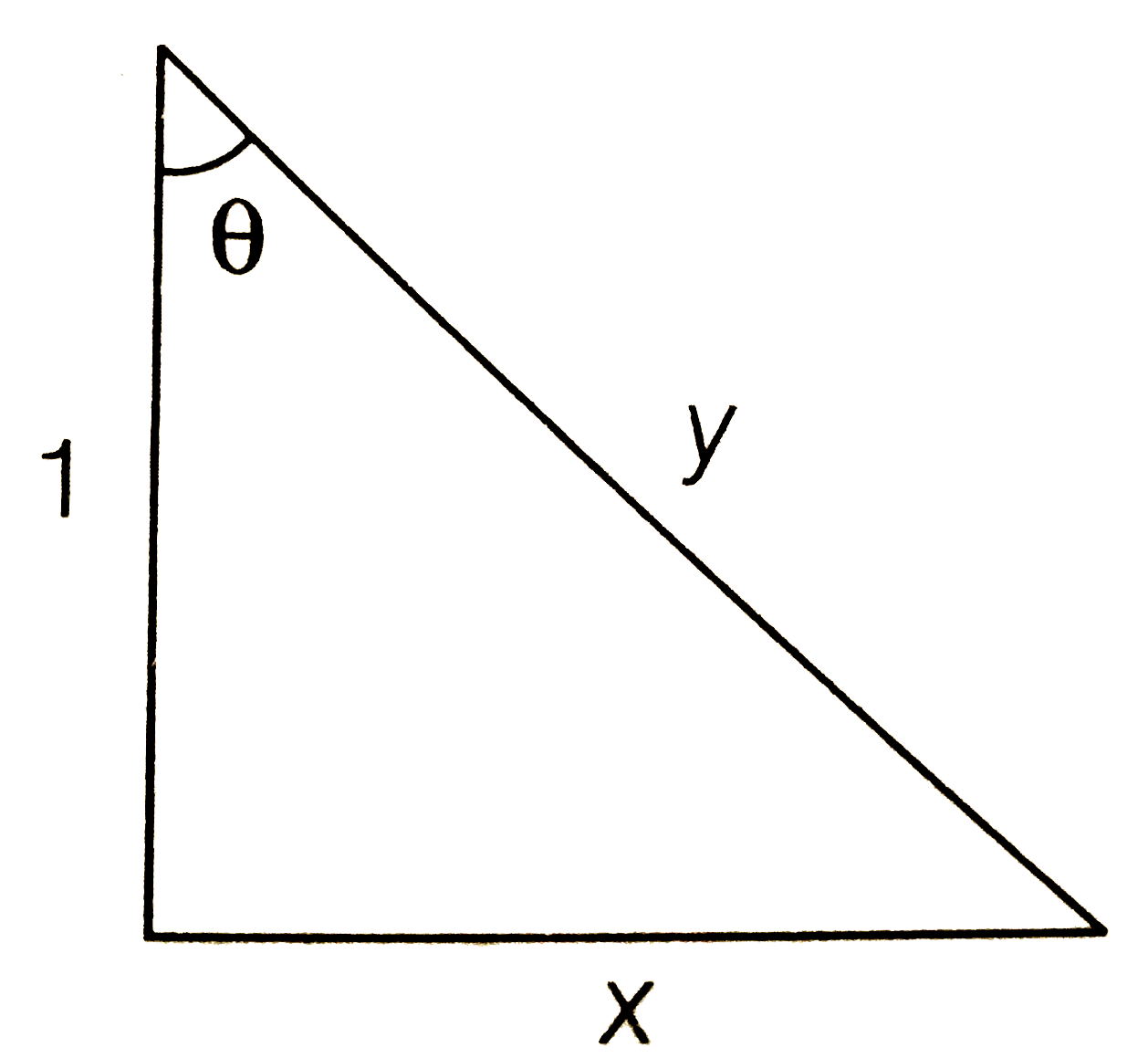
 View Solution
View SolutionFind the area of an isosceles right triangle whose hypotenuse is 4√2 cm
View SolutionThe area of an isosceles right triangle is 200 m^2. Find its hypotenuse.
View SolutionThe equation of the circumcircle of the triangle, the equation of whose sides are y=x,y=2x,y=3x+2, is
View SolutionFind the equations of the medians of a triangle, the equations of whose sides are: 3x+2y+6=0, 2x−5y+4=0 and x−3y−6=0
View Solution

