A square loop EFGH of side a, mass m and total resistance R is falling under gravity in a region of transverse non - uniform magnetic field given by B=By0a =, where B0 is a positive constant and y is the position of side EF of the loop. If at some instant the speed of the loop is v, then the total Lorentz acting on the loop is

F=B20a2v2H
F=2B20a2vR
F=B20a2vR
zero
The correct Answer is:C
Step by step video & image solution for A square loop EFGH of side a, mass m and total resistance R is falling under gravity in a region of transverse non - uniform magnetic field given by B=B_(0)^(y)/(a) =, where B_(0) is a positive constant and y is the position of side EF of the loop. If at some instant the speed of the loop is v, then the total Lorentz acting on the loop is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A square loop ABCD of side l is moving the xy plane with velocity →v=βtˆj.There exists a non-uniform magnetic field →B=−B0(1+αy2)ˆk(y>0), where B0 and α are positive constants. Initially, the upper wire of the loop is at y=0.Find the induced voltage across the resistance R as a function of time.Neglect the magnetic force due to induced current.

View SolutionA magnetic field B=B0(y/a)(^)k is into the paper in the +z direction, B0 and a are positive constants. A square loop EFGH of side a, mass m and resistance R, in x-y plane, starts falling under the influence of gravity see figure. Note the direction of x and y axis in figure.
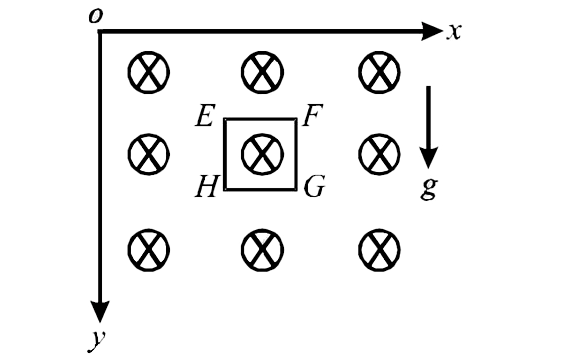
Find
(a) the induced current in the loop and indicate its direction.
(b) the total Lorentz force acting on the loop and indicate its direction, and
(c) an expression for the speed of the loop, v(t) and its terminal value.
View Solution
Knowledge Check
The magnetic field I nan reigion is given by B=B0XaK. A Squrae edges along the x and y axis. The loop is moved with a constant velocity . The emf induced in the loop is
 AB0v0dBB0v0d22aCB0v0d3a2DB0v0d2a
AB0v0dBB0v0d22aCB0v0d3a2DB0v0d2aA square loop of side 'a' is placed in x−y plane as shown in figure. In this region there is non-uniform time dependent magnetic field →B=(cy3t2)→k, [where t is time and c is constant] then magnitude of emf induced in loop is
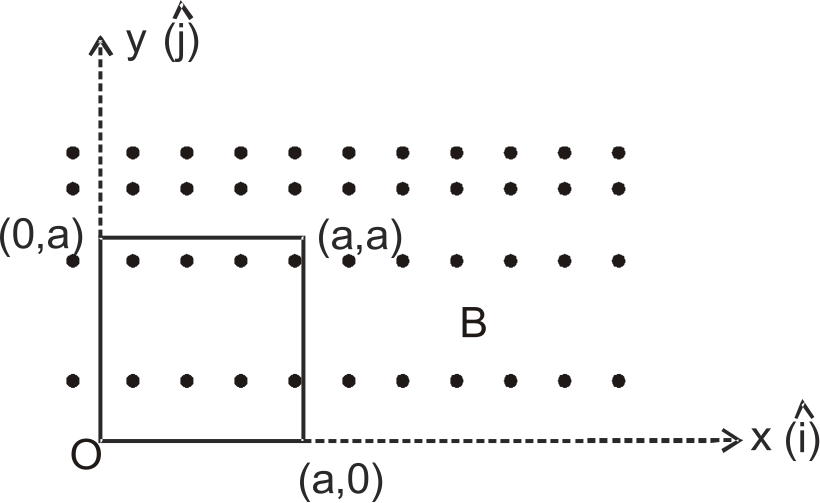 AZeroBca4t25Cca5t2Ddata is insufficient
AZeroBca4t25Cca5t2Ddata is insufficientA circular loop of radius R carrying current I is kept in XZ plane. A uniform and constant magnetic field →B=(B0ˆi+2B0ˆj+3B0ˆk) exists in the region (B0− a positive constant). Then the magnitude of the torque acting on the loop will be
A2IπR2B0B√5IπR2B0C√10IπR2B0D6IπR2B0
A square loop of edge a has N turns and a total resistance R . The loop moves with constant velocity v through a region of constant magnetic field B . The loop enters in magnetic field at t=0. Discuss the vartion of (a) Flux passing through the loop (b) the induced emf and (c) the external force acting on the loop a function of position of the loop in the field.

View SolutionA square metal wire loop of side 10 cm and resistance 1 ohm is moved with a constant velocity (v0) in a uniform magnetic field of induction B=2weber/m2 as shown in the figure. The magnetic field lines are perpendicular to the plane to the loop (directed into the paper). The loop is connected to a network of resistors each of value 3 ohms. The resistances of hte lead wire OS and PQ are negligible. What should be the speed of the loop so as to have a steady current of 1 milliampere in the loop? Given the direction of current in the loop.
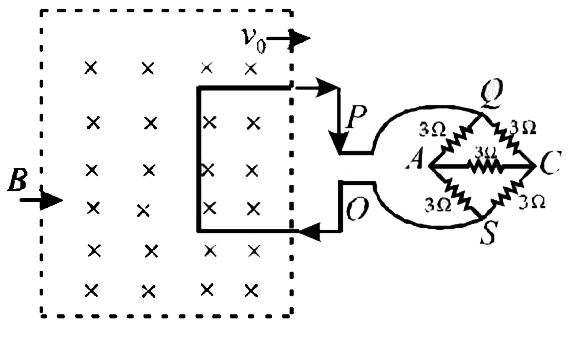
View SolutionA rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnitude 0.20 T exists parallel to the longer side of the loop (a) What is the force acting on the loop? (b) what is the torque acting on the loop?
View SolutionA square loop of side a and resistance B is moved in the region of uniform magnetic field B (loop remaining completely inside field), with a velocity v through a distance x. The work done is
View SolutionA square loop of side a and resistance R is moved in the region of uniform magnetic field B(loop remaining completely insidefield), with a velocity v through a distance x. The work done is:
View Solution
