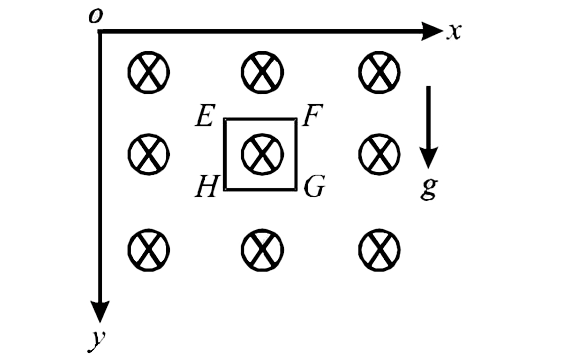
A magnetic field is into the paper in the +z direction, and a are positive constants. A square loop EFGH of side a, mass m and resistance R, in x-y plane, starts falling under the influence of gravity see figure. Note the direction of x and y axis in figure.
Find
(a) the induced current in the loop and indicate its direction.
(b) the total Lorentz force acting on the loop and indicate its direction, and
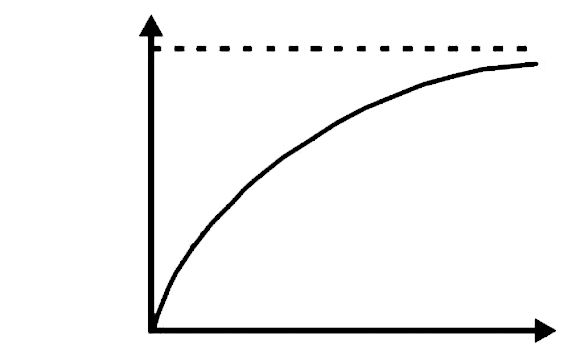
(c) an expression for the speed of the loop, v(t) and its terminal value.
The correct Answer is:A, B, C, D
Suppose at
(a) Total magnetic flux=
where
Net emf.
As total resistance =R
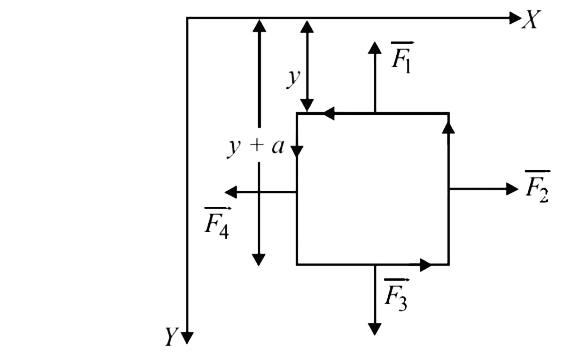
(b) Each side of the cube will experience a forve as shown (since a current carrying segment in a magnetic field experience a force).
(c) Total net force =
Integrating it we get,
or log [(g-(B_(0)^(2)a^(2)v(t))/(mR))/(g)]=-(B_(0)^(2)a^(2))/(mR)1-(B_(0)^(2)a^(2)v(t))/(mgR))=e^(-(B_(0)^(2)a^(2)t)//(mR)oe, 1-=e^(-(B_(0)^(2)a^(2)t)//(mR)
When terminal velocity is attained, v(t) does not depend on t
Topper's Solved these Questions
Similar Questions
A square loop EFGH of side a, mass m and total resistance R is falling under gravity in a region of transverse non - uniform magnetic field given by B=By0a =, where B0 is a positive constant and y is the position of side EF of the loop. If at some instant the speed of the loop is v, then the total Lorentz acting on the loop is
View SolutionA circular brass loop of radius a and resistance R is placed with it plane perpendicular to a magnetic field, which varies with time as B=B0sinωt. Obtain the expression for the induced current in the loop.
View Solution
Knowledge Check
A magnetic field B=(B0y/a)ˆk is acting into the paper in the +z direction. B0 and a are positive constants. A square loop EFGH of side a, mass m and resistance R kept in x-y plane starts faling under the influcence of gravity.Note the directions of x and y in the figure.
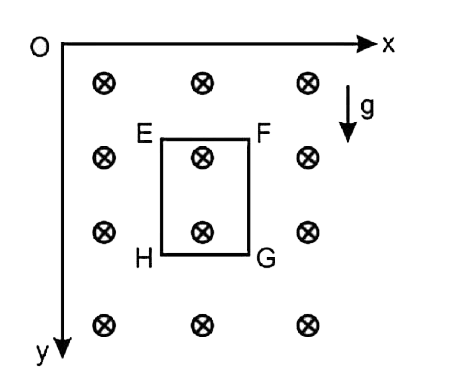
Find the induced current in the loop and indicate its direction.Ai=B0avR and direction of current will be counter clockwiseBi=RB0av and direction is counter clockwiseCi=B0avR and direction is clockwiseDi=RB0av and direction is clockwiseA magnetic field B=(B0y/a)ˆk is acting into the paper in the + z direction. Bo and a are positive constants. A square loop EFGH of side a, mass m and resistance R kept in x-y plane starts falling under the influence of gravity. Note the directions of x and y in the figure.
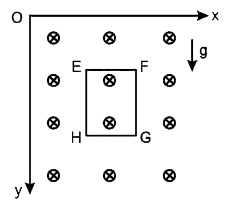
Find the total Lorentz force acting on the loop and indicate its direction.A→F=B20a2vRˆj upwardsB→F=B20a2vRˆj downwardsC→F=B20a2vRˆj upwardsD→F=B20a2vRˆj downwardsThe current flows from A to B as shown in the figure The direction of the induced current in the loop is :
 AclockwiseBanticlockwiseCstraight lineDnone of these
AclockwiseBanticlockwiseCstraight lineDnone of these
A circular loop of radius R=20 cm is placed in a uniform magnetic field B=2T in xy-plane as shown in figure. The loop carries a current i=1.0A in the direction shown in figure. Find the magnitude of torque acting on the loop.
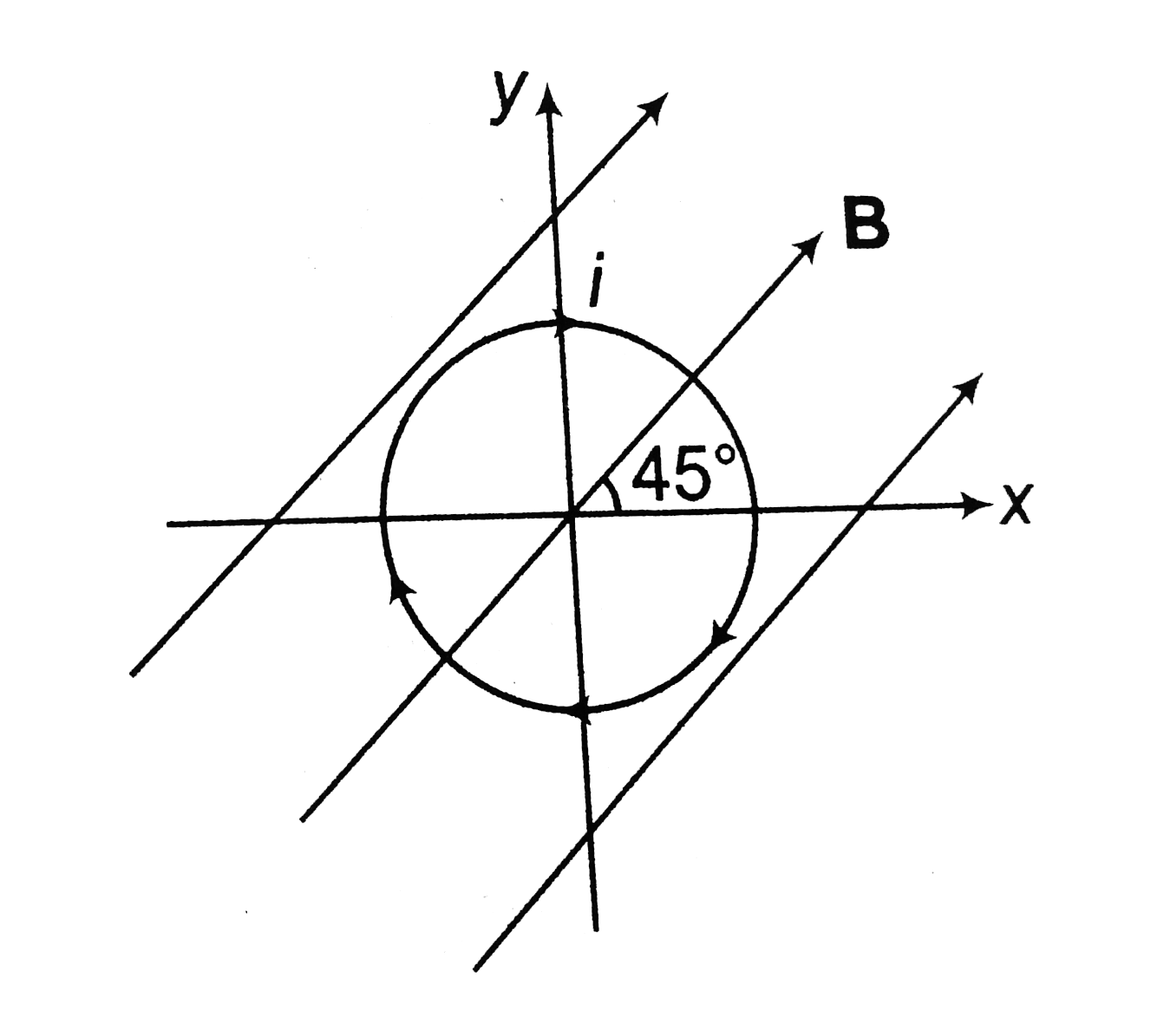
View SolutionA current carrying circular loop of radius R is placed in a uniform magnetic field B0 Tesla in x-y plane as shown in figure. The loop carries a current i=1A in the direction shown. Find the torqure acting on the loop
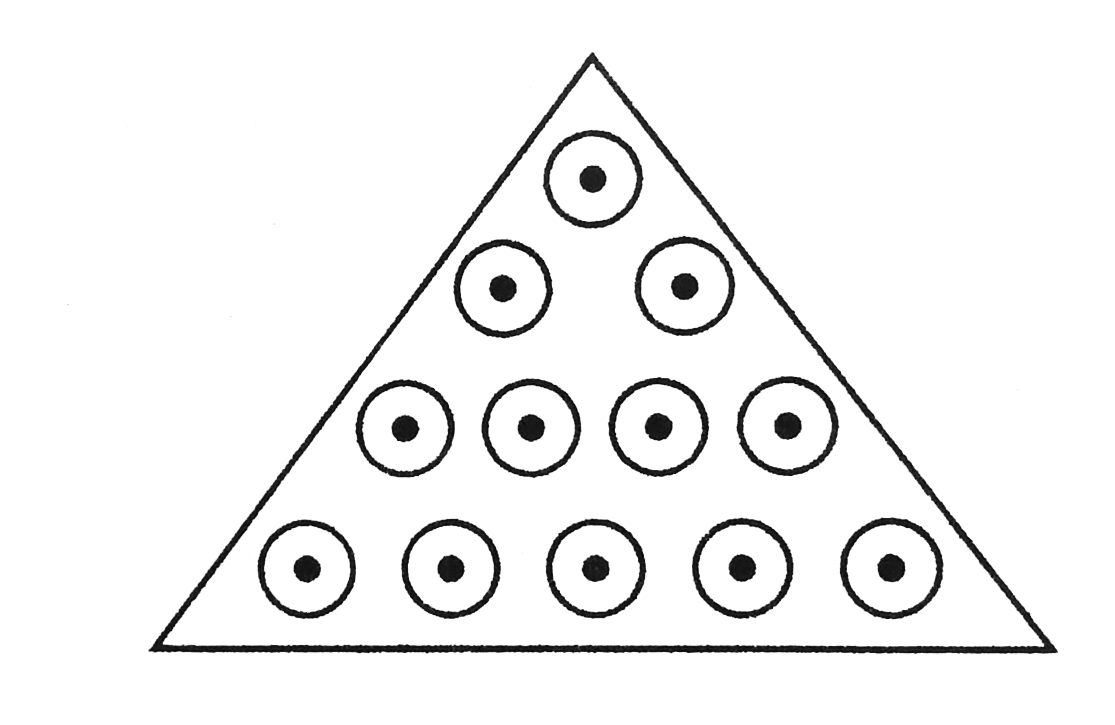
View SolutionA triangular loop is placed in a dot ⊙ magnetic field as shown in figure. Find the direction of induced current in the loop if magnetic field is increasing.
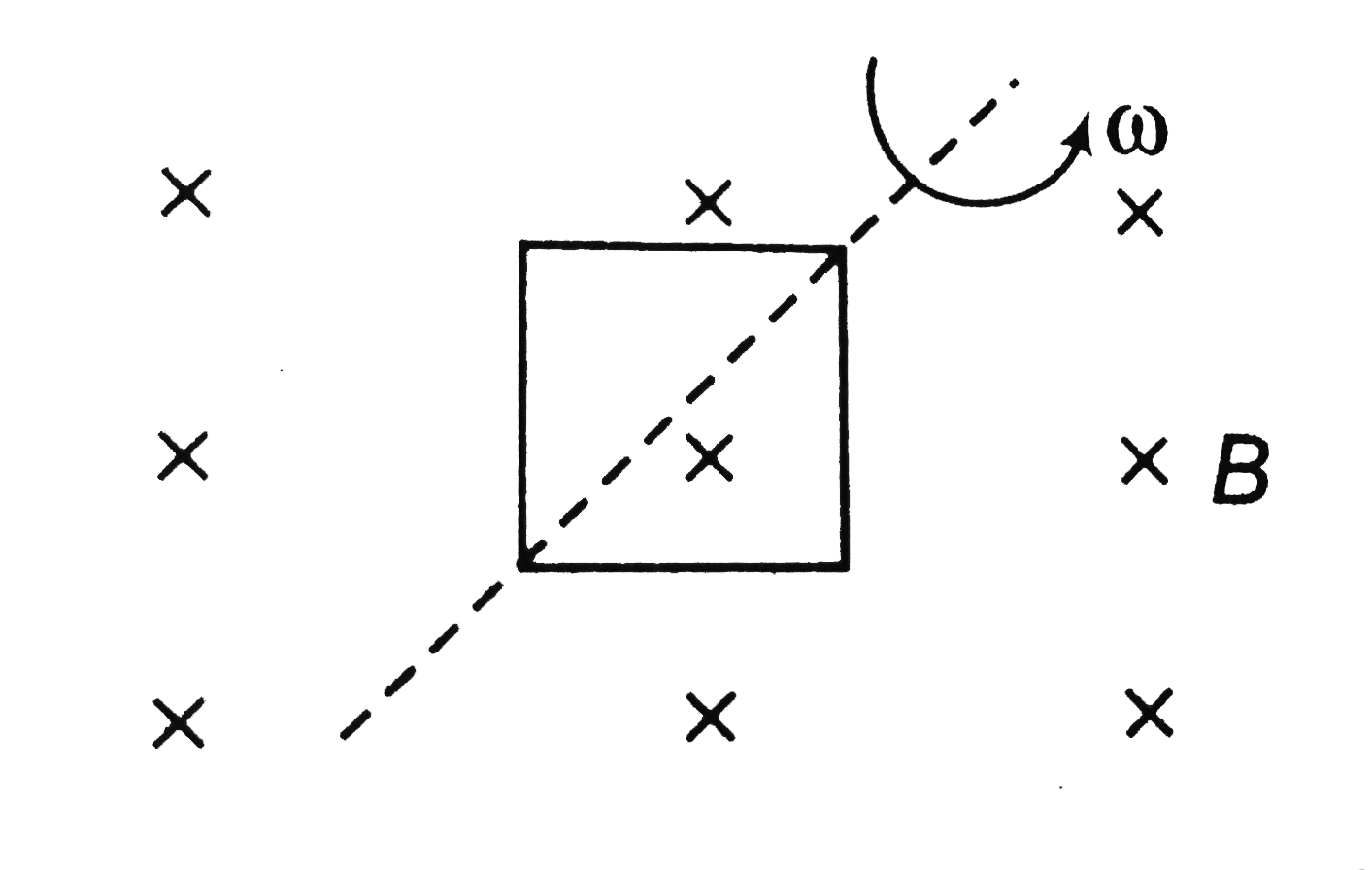
View SolutionA square loop of side b is rotated in a constant magnetic field B at angular frequency ω as shown in the figure. What is the emf induced in it?
View SolutionA circular loop of wire is positioned half in and half out of a square region of uniform magnetic field directed in the +z direction, out of the paper, as shown in the following figure. To induce a counterclockwise current in this loop
View Solution
