A small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
Actual depth of the bulb in water, d1=80cm=0.8m
Refractive index of water, μ=1.33
The given situation is shown in the following figure.
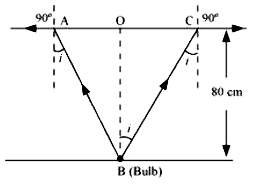
Where, i=Angle of incidence
r = Angle of refraction = 90∘.
Since,the bulb is a point source, the emergent light can be considered as a circle of
R=AC2=AO=OB
radius, Using Snell's law, we can write the relation for the refractive index of water as:
μ=sinrsini
1.33=sin90∘sini
∴i=sin−1(11.33)=48.75∘
using the given figure, we have the relation,
tani=OCOB=Rd1
R=tan48.75∘×0.8=0.91m
Area of the surface of water = nR2=n(0.91)2=2.61m2
Hence, the area of the surface of water through which the light from the bulb can emerge is approximately 2.62 m2.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERTCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise
32 Videos
- NUCLEIBOOK - NCERTCHAPTER - NUCLEIEXERCISE - Exercise
31 Videos
- SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITSBOOK - NCERTCHAPTER - SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITSEXERCISE - Exercise
15 Videos
Similar Questions
A small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33. [Consider the bulb to be a point source]
View SolutionA small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. What is the area of the surface of water through which light from the bulb can emerge out? (Refractive index of water is 1.33. (Consider the bulb to be a point source)
View Solution
Knowledge Check
A small bulb is placed at the bottom of a tank containing water to a depth of 80cm. What is the area of the bulb can emerge out? Refractive index of water is 1.33. (Consider the bulb to be a point source.)
A3.13 m2B1.43 m2C2.61m2D0.88m2A point source of light is placed at the bottom of a water lake. If the area of the illuminated circle on the surface is equal to 3 times the square of depth of the lake, the refractive index of water.
A√π+1B√π3+1Cπ3+1Dπ4+1
A cylindrical tank 7m in diameter, contains water to a depth of 4m. What is the total area of wetted surface
View SolutionA point source of light is placed on the bed of a pond 80 cm deep. Find the diameter of the liuminatded circle on the surface of water.
View SolutionA point source of light is 80.0cm below the surface of a body of water. Find the diameter of the circle at the surface through which light emerges from the water.
View SolutionA point source is placed at a depth h below the surface of water (refractive index =μ). The medium above the surface of water is air from water.
View SolutionAn isotropic point source is placed at a depth h below the water surface. A floating opaque disc is placed on the surface of water so that the source is not visible from the surface. What is the minimum radius of the disc? Take refractive index of water=μ.
View SolutionA rectangular tank 8m deep is full of water. By how much does the bottom appear to be raised if the refractive index of water is 4/3?
View Solution
