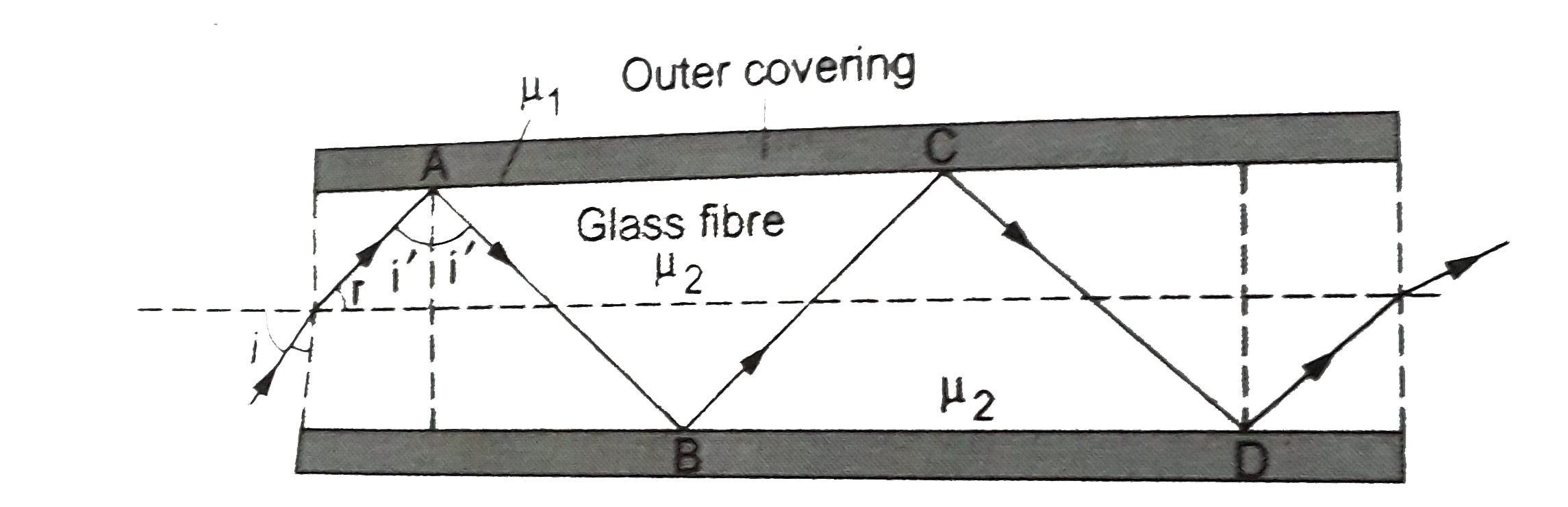
(a) Fig. shows a cross-section of a 'light pipe' made of a glass fiber of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the axis of the pipe for which total reflection inside the pipe take place as shown.
(b) What is the answer if there is no outer covering if the pipe ?
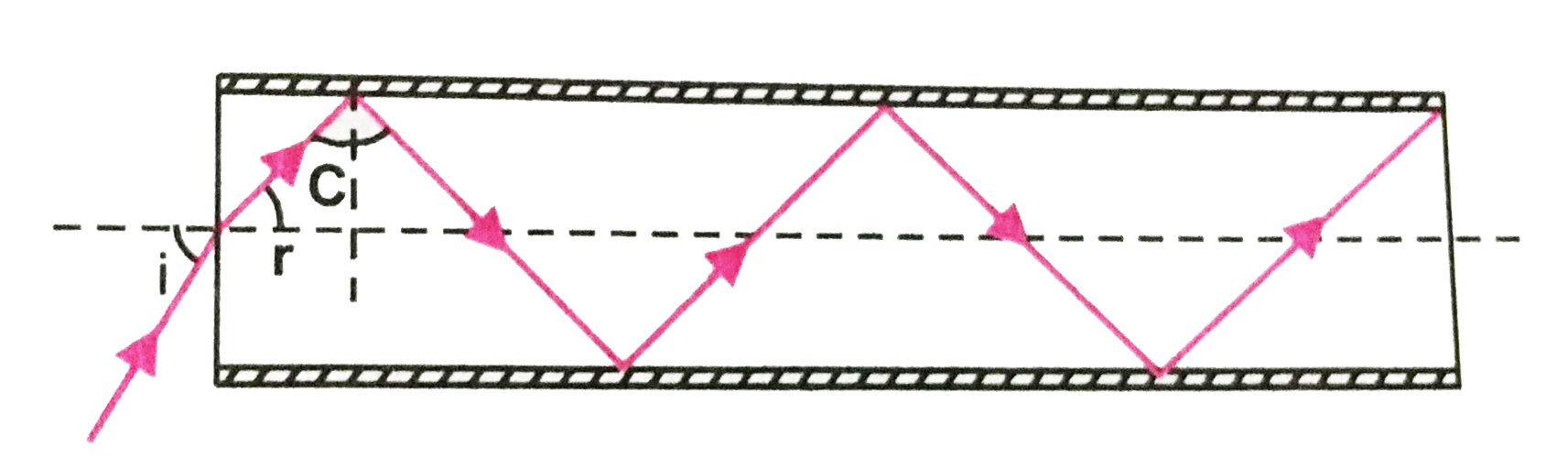
a) Refractive index of the glass fibre, μ1=1.68
Refractive index of the outer covering of the pipe, μ2=1.44
Angle of incidence =I
Angle of refraction =r
Angle of incidence at the interface =i′
The refractive index (μ) of the inner core-outer core interface is given as:
μ=μ2μ1=1sini
sini=μiμ2
−1.441.68=0.8571
∴i′=59∘.
For the critical angle, total internal reflection (TIR) takes place only when i>i′ , i.e., i>59∘.
Maximum angle of reflection, rmax=90∘−i′=90∘−59∘=31∘
Let, imax be the maximum angle of incidence.
The refractive index at the air-glass interface, μi=1.68
We have the relation for the maximum angles of incidence and reflection as:
μi=sinimaxsinrmax
sinimax=μisinrmax
=1.68sin31∘
=1.68×0.5150
=0.8652
∴imax=sin−10.8652≈60∘.
Thus, all the rays incident at angles inthe range 0<i<60∘.
thus, all the rays incident at angles lying in the range 0<i<60∘ will suffer total internal reflection.
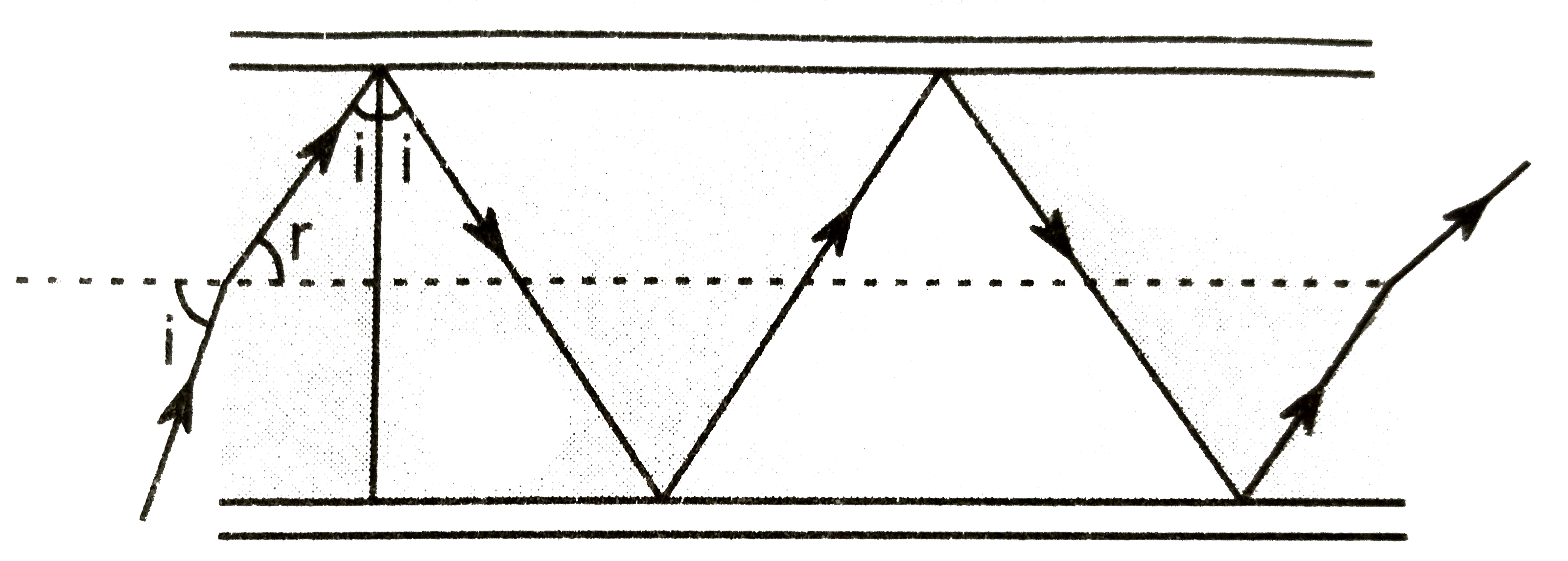
b) If the outer covering of the pipe is not present, then,
Refractive index of the outer pipe, μi= Refractive index of air=1
For the angle of incidence i=90∘, we can write Snell's law at the air - pipe interface as:
sinisinr=μ2=1.68
sinr=sin90∘1.68=11.68
r=sin−1(0.p5952)
=36.5∘
∴i′=90∘−p36.5∘ = 53.5∘
Since, i′>r, all incident rays will suffer total internal reflection.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise32videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - NCERTCHAPTER - NUCLEIEXERCISE - Exercise31videos
NUCLEI
- BOOK - NCERTCHAPTER - SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITSEXERCISE - Exercise15videos
SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
A small candle 2.5cm in size is placed 27cm in front of a concave mirror of radius of curvature 36cm. At what distance from the mirror should a screen be placed in order to receive a sharp image ? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved ?
12:38View Solution(a) Two stable isotope of .3Li6 and .3Li7 have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 and 7.01600 u respectively. Find the atomic weight of lithium.
(b) Boron has two stable isotopes .5B10 and .5B11. Their respective masses are 10.01294 u and 11.00931 u, and the atomic weight of boron is 10.81 u. Find the abundances of .5B10 and .5B11.06:58View SolutionIn a n-type semiconductor, which of the following statement is true?
03:27View Solution(a) Fig. shows a cross-section of a 'light pipe' made of a glass fibre of refractive index 1.68 . The outer covering of the pipe is made of a material of refractive index 1.44 . What is the axis of the pipe for which total reflection inside the pipe take place as shwon. (b) What is the answer if there is no outer covering if the pipe ?
08:18View Solutionचित्र में अपवर्तनांक 1.68के तन्तु काँच से बनी किसी 'प्रकाश नलिका' (लाइट पाइप) का अनुपर्ष्ठ परिच्छेद दर्शाया गया है| नलिका का बाह्य आवरण 1.44अपवर्तनांक के पदार्थ का बना है| नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण प्रवर्तन होते है, ज्ञात कीजिए |
(b) यदि पाइप पर बाह्य आवरण न हो तो क्या उत्तर होगा ?View Solution14 cm लम्बे धातुई पाइप के बाहरी एव भीतरी क्षेत्रफलों का अंतर 88cm2 है यदि पाइप 198cm3 धातु से बना है तो पाइप का भीतरी एवं बाहरी त्रिज्या ज्ञात करे।
 12:38View Solution
12:38View Solution(a ) चित्र में अपवर्तनांक 1.68 के काँच तंतु से बनी किसी प्रकाश नालिका का अनुप्रस्थ परिच्छेद दर्शाया गया है। नलिका का बाह्य आवरण ( outer covering ) 1.44 अपवर्तनांक के पदार्थ का बना है। नालिका के अक्ष से आपतित किरणों के कोनों का परिसर ( range ), जिनके लिए चित्र में दर्शाए अनुसार नालिका के भीतर पूर्ण परावर्तन होते है, ज्ञात कीजिए।
(b ) यदि पाइप पर बाह्य आवरण न हो, तो क्या होगा ?
 View Solution
View Solutionचित्र में अपवर्तनांक 1⋅68 के तंतु काँच से बनी किसी 'प्रकाश नलिका' (लाइट पाइप) का अनुप्रस्थ परिच्छेद दर्शाया गया है| नलिका का बाहा आवरण 1⋅44 अपवर्तनांक के पदार्थ का बना है| नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण परावर्तन होते है ज्ञात कीजिए |
06:32View Solution(a) Fig. shows a cross-section of a 'light pipe' made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the axis of the pipe for which total reflection inside the pipe take place as shwon.
(b) What is the answer if there is no outer covering if the pipe ?
 05:45View Solution
05:45View SolutionWhat is the answer if there is no outer covering of the pipe?
06:04View Solutiona.Figure shows a cross-section of a 'light pipe' made of glass fibre of refractive index 1.68
The outer converting of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections insides the pipe take place as shown in the figure.
b.What is the answer if there is no outer converting of the pipe ?
 06:45View Solution
06:45View SolutionA optical fiber is made up of a core material with refractive index 1.68 and a cladding material of refractive index 1.44. What is the acceptance angle of the fiber kept in air medium? What is the answer if there is no cladding?
06:52View SolutionCross section of a light pipe is shown in the following figure :

Inner core is material of refractive index 1.68 and its outer covering is a material of refractive index 1.44. Find the maximum angle at which the ray can be incident with the axis of pipe for which total internal reflection occurs inside the pipe.View Solution(a) Figure 9.32 shows a cross-section of a 'light pipe' made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure.
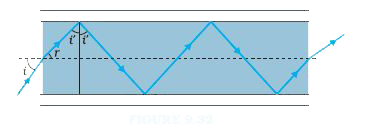
(b) What is the answer if there is no outer covering of the pipe?04:21View Solution(a) Figure 9.32 shows a cross-section of a 'light pipe' made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure.
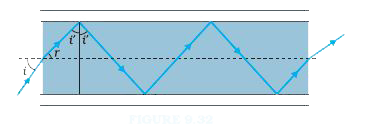
(b) What is the answer if there is no outer covering of the pipe?View Solution(a) Fig. 9.04 shows a cross-section of a Tight pipe' made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure.
(b) What is the answer if there is no outer covering of the pipe ?
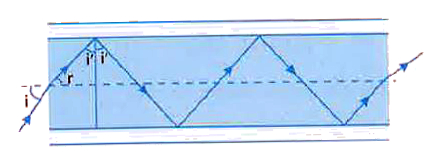 07:10View Solution
07:10View Solution

