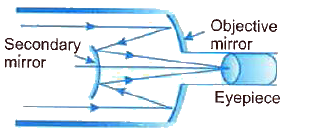
A Cassegrainian telescope uses two mirrors as shown in Fig. Such a telescope is built with the mirrors $20 m m$ apart. If the radius of curvature of large mirror is $220 m m$ and the small mirror is $40 m m$ , where will the final image of an object at infinity be ?

Video Solution

Text Solution

Verified by Experts

The following figure shows a Cassegrain telescope consisting of a concave mirror and a convex mirror.
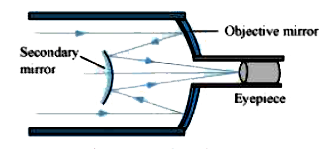Distance between the objective mirror and the secondary mirror, d=20mm Radius of curvature of the secondary mirror, R1=140mm
Hence, focal length of the secondary mirror, $f_{2} = \frac{R_{2}}{2} = \frac{140}{2} = 70 m m$
The image of an object placed at infity, formed by the objective mirror, will act as a virtual object for the secondary mirror. Hence, the virtual object distance for the secondary mirror, $μ = f_{1} - d$
$110 - 20 = 90 m m$
Applying the mirror formula for the secondary mirror, we can calculate image distance (v) as
$\frac{1}{v} + \frac{1}{u} = \frac{1}{f_{2}}$
$\frac{1}{v} = \frac{1}{f_{2}} - \frac{1}{u}$
$- \frac{1}{70} - \frac{1}{90} = \frac{9 - 7}{630} = \frac{2}{630}$
$∴ v = \frac{630}{2} = 315 m m$
Hence, the final image will be formed 315 mm away from the secondary mirror.

Updated on:21/07/2023

A convex mirror forms a real image $5$ times the size of the object placed at a distance of $20$ cm from it. The radius of curvature of the mirror is
A $\frac{100}{3} c m$
B $\frac{50}{3} c m$
C $100 c m$
D $50 c m$
An object is 100 mm in front of a concave mirror which produces an upright image (erect image). The radius of curvature of the mirror is :
Aless than 100 mm
Bbetween 100 mm and 200 mm
Cexactly 200 mm
Dmore than 200 mm
A slab of glass, of thickness 6 cm and refractive index 1.5, is placed in front of a concave mirror, the faces of the slab being perpendicular to the principal axis of the mirror. If the radius of curvature of the mirror is 40 cm and the reflected image coincides with the object, then the distance of the object from the mirror is
A30 cm
B22 cm
C42 cm
D28 cm