A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t=0. Determine the amplitude of the resulting oscillations in terms of the parameters ω,x0andv0.
x=αcos(ωt+θ)
v=dxdt=−aωsin(ωt+θ)
when t=0,x=x0 and dxdt=−v0
∴X0=acosθ.....(i)
and −v0=−aωsinθ or asinθ=v0ω....(ii)
Squaring and adding (i) and (ii) , we get
a2(cos2θ+sin2θ)=x20+v20ω2
or a=
⎷(x20+v20ω2)
Topper's Solved these Questions
Similar Questions
Knowledge Check
A mass attached to a string rotates about a fixed centre with an angular velocity ω in a horizontal plane ,The length of the string and the angular velocity are now doubled .IF T0 is the initial tension in the string , then the new tension will be
A2T0B4T0C8T0D6T0A solid sphere with a velocity (of centre of mass) v and angular velocity ω is gently placed on a rough horizontal surface. The frictional force on the sphere :
Amust be forward (in direction of v)Bmust be backward (opposite to v)Ccannot be zeroDnone of the aboveA block of mass m is pushed towards the movable wedge of mass M and height h, with a velocity v0. All surfaces are smooth . The minimum value of v0 for which the block will reach the top of the wedge is
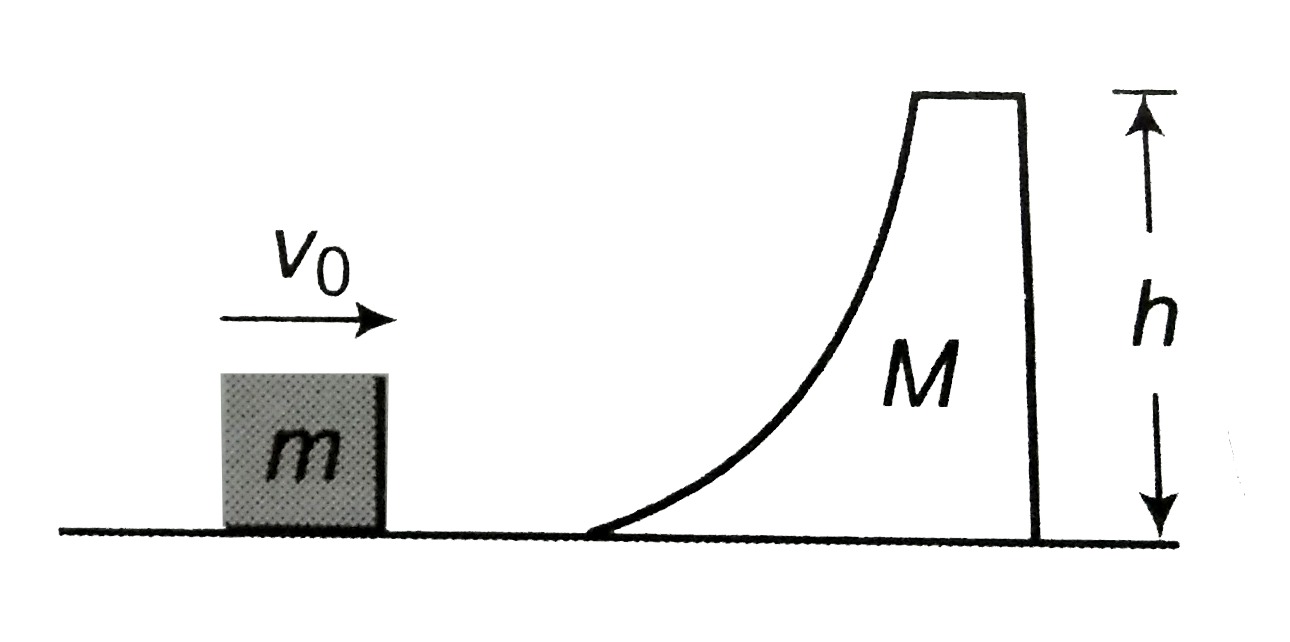 A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M)
A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M)
Find the angular frequency and the amplitude of harmonic oscillations of a particle if at distances x1 and x2 from the equalibrium position its velocity equald v1 and v2 respectively.
View SolutionA block of mass 1 kg attached to a spring is made to oscillate with an initial amplitude of 12 cm. After 2 minutes the amplitude decreases to 6 cm. Determine the value of the damping constant for this motion. (take In 2 =0.693 )
View SolutionA mass M attached to a spring of spring constant 0.7 N/m oscillates on a smooth horizontal table. When displacement is 0.3 m, velocity is 2 ms−1. And when displacement is 0.4 m, velocity is 0.3 m/s. Calculate the vlaue of M.
View SolutionA uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.

View SolutionA billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
View Solution