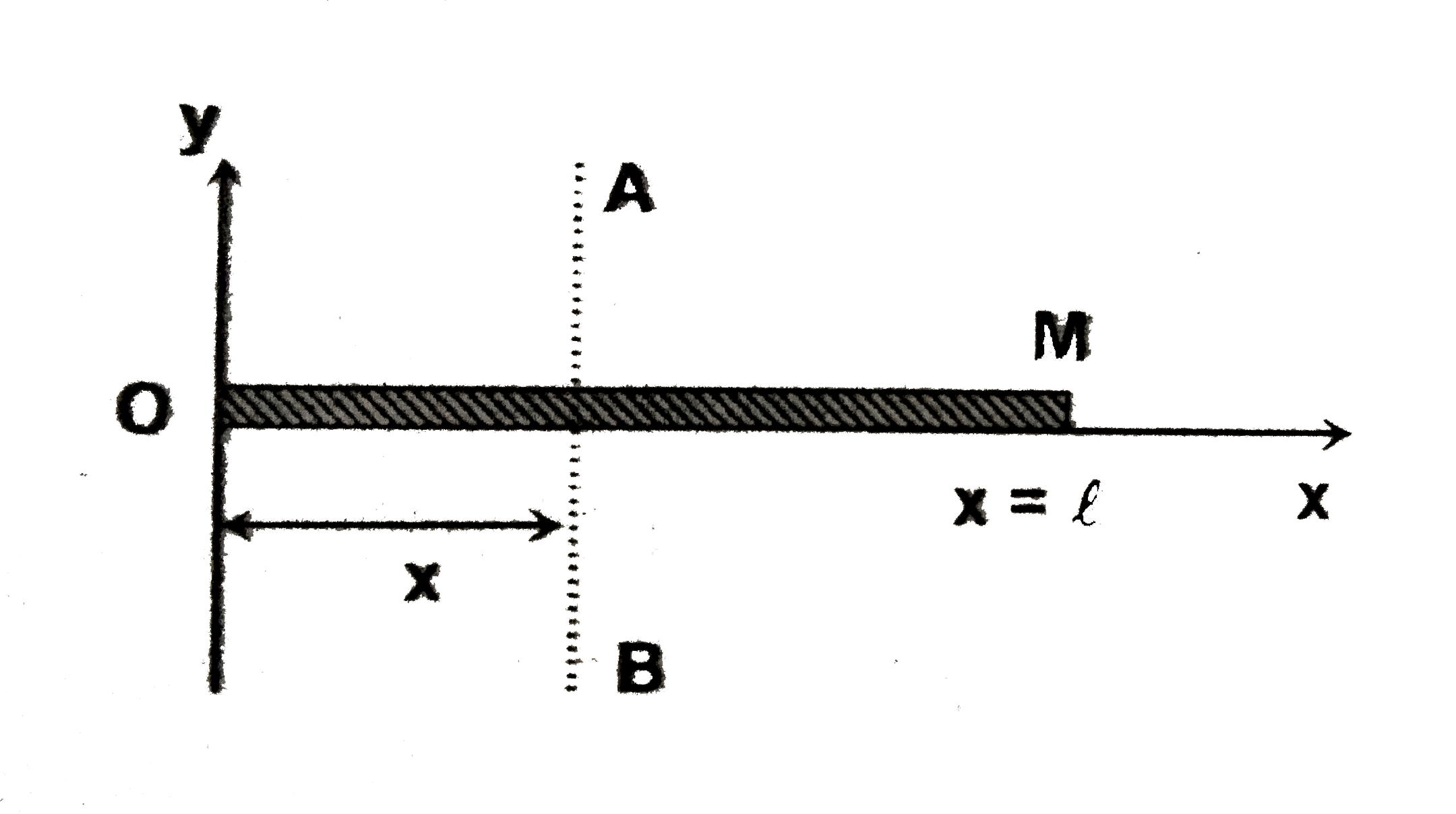
A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass density that varies with the distance x from left end of the rod according to λ=λ0(x3L3)
Where unit of λ0 is kg/m. What is the value of x so that moment of inertia of rod about axis AB (IAB) is minimum?
7l15
2l5
8115
4l5
The correct Answer is:D
Step by step video, text & image solution for A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass density that varies with the distance x from left end of the rod according to lamda=lamda_(0)((x^(3))/(L^(3))) Where unit of lamda_(0) is kg/m. What is the value of x so that moment of inertia of rod about axis AB (I_(AB)) is minimum? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Linear mass density of a rod AB ( of length 10 m) varied with distance x from its end A as λ=λ0x3 (λ0 is positive constant). Distance of centre of mass the rod, form end B is
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View Solution
Knowledge Check
A rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass?
 A23LB14LC13LD12L
A23LB14LC13LD12LA rod of length 2 m, has a mass of 0.12 kg. Its moment of inertia about an axis passing through its one end and perpendicular to the length of the rod is
A0.16 kg - m2B0.12 kg - m2C0.32 kg - m2D0.08 kg - m2A non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
AL/2B2L/3CL/4DL/5
A non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is λ=λ0x. The centre of mass of rod divides the length of the rod in the ratio:
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionThe linear mass density of a thin rod AB of length L varies from A to B as λ(x)=λ0(1+xL). Where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicualr to the rod is :
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
View Solution
