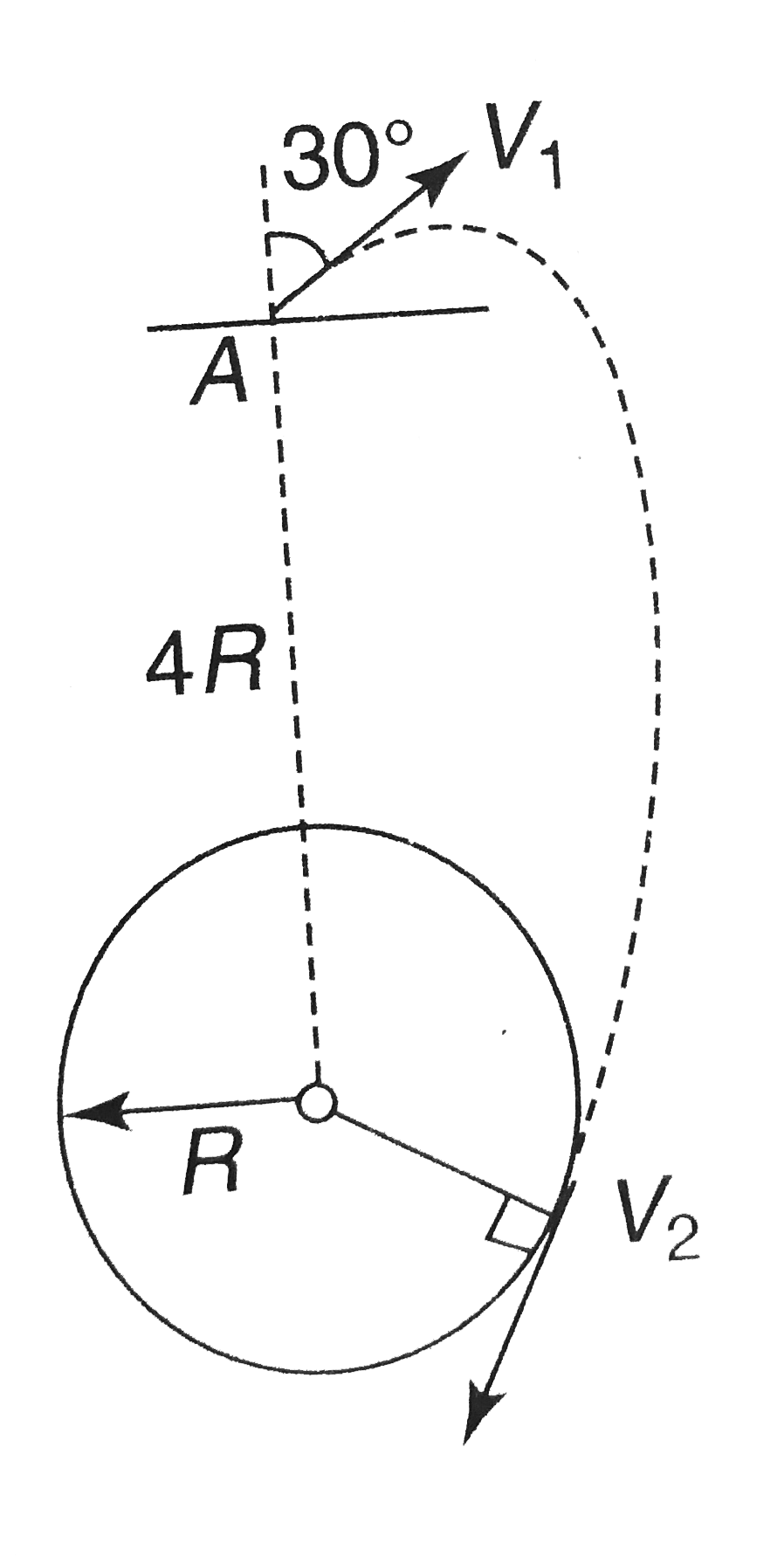
A particle is projected from point A, that is at a distance 4R form th

A body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
A $\sqrt{\frac{2 G M}{R}}$
B $\sqrt{\frac{2 G M}{R - r}}$
C $\sqrt{\frac{2 G M (r - R)}{R r}}$
DZero
A particle is projected vertically with speed V from the surface of the earth . Maximum height attained by the particle , in term of the radius of earth R,V and g is ( V $<$ escape velocity , g is the acceleration due to gravity on the surface of the earth )
A $\frac{3 R V^{2}}{2 g R - 2 V^{2}}$
B $\frac{2 R V^{2}}{3 g R - V^{2}}$
C $\frac{R V^{2}}{2 g R - V^{2}}$
D $\frac{R V^{2}}{g R - 2 V^{2}}$
If $d$ is the distance between the centre of the earth of mass $M_{1}$ and the moon of mass $M_{2}$ , then the velocity with which a body should be projected from the mid point of the line joining the earth and the moon, so that it just escape is
A $\frac{\sqrt{G (M_{1} + M_{2})}}{d}$
B $\sqrt{\frac{G (M_{1} + M_{2})}{2 d}}$
C $\sqrt{\frac{2 G (M_{1} + M_{2})}{d}}$
D $\sqrt{\frac{4 G (M_{1} + M_{2})}{d}}$

The correct Answer is:A