A particle is projected from point A, which is at a distance 4R from the centre of the earth, with speed v1 in a direction making 30∘ with the line joining the centre of the earth and point A, as shown. Find the speed v1 if particle passes grazing the surface of the earth. Consider gravitational interaction only between these two. Express you answer in the form 1000X√2~ms and find value of X. (Use GMR= 6.4×107m2s2 )
'(##CEN_KSR_PHY_JEE_C10_033_Q03##)'
The correct Answer is:8
Topper's Solved these Questions
Similar Questions
A particle is projected from point A, that is at a distance 4R form the centre of the earth, with speed V1 in a direction making 30∘ with the line joining the centre of the earth and point A, as shown. Consider gravitational interaction only between these two. (Use GMR=6.4×107m2/s2). The speed V1 if particle pasess grazing the surface of the earth is
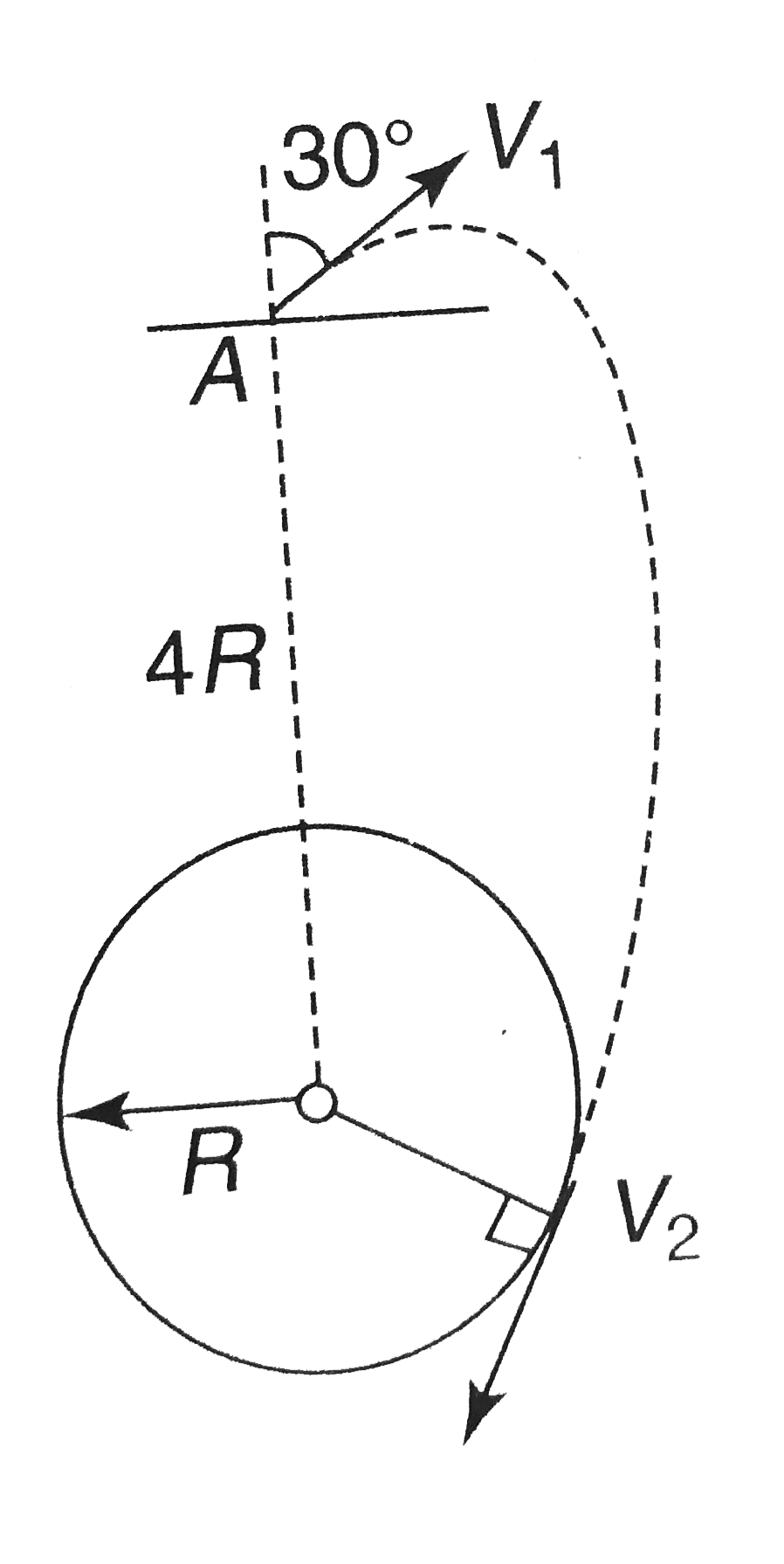
View SolutionA particle is projected from point A, that is at a distance 4R form the centre of the earth, with speed V1 in a direction making 30∘ with the line joining the centre of the earth and point A, as shown. Consider gravitational interaction only between thesetwo. (Use GMR=6.4×107m2/s2). The speed V1 if particle pasess grazing the surface of the earth is

View Solution
Knowledge Check
A particle is projected from point A, that is at a distance 4R form the centre of the earth, with speed V1 in a direction making 30∘ with the line joining the centre of the earth and point A, as shown. Consider gravitational interaction only between thesetwo. (Use GMR=6.4×107m2/s2). The speed V1 if particle pasess grazing the surface of the earth is
 A2√2×103m/sB4√2×103m/sC4×103m/sD4√3×103m/s
A2√2×103m/sB4√2×103m/sC4×103m/sD4√3×103m/sA body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
A√2GMRB√2GMR−rC√2GM(r−R)RrDZeroThe distance of the centres of moon the earth is D. The mass of earth is 81 times the mass of the moon. At what distance from the centre of the earth, the gravitational force on a particle will be zero.
AD2B2D3C4D3D9D10
A body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
View SolutionIf r the distance from the centre of the earth, then what is the nature of the graph of gravitational acceleration versus r for point below the earth's surface?
View SolutionThe distance of the centres of moon the earth is D. The mass of earth is 81 times the mass of the moon. At what distance from the centre of the earth, the gravitational force on a particle will be zero.
View SolutionA particle is given a velocity ve√3 in a vertically upward direction from the surface of the earth, where ve is the escape velocity from the surface of the earth. Let the radius of the earth be R. The height of the particle above the surface of the earth at the instant it comes to rest is :
View SolutionA particle is given a velocity ve√3 in a vertically upward direction from the surface of the earth, where ve is the escape velocity from the surface of the earth. Let the radius of the earth be R. The height of the particle above the surface of the earth at the instant it comes to rest is :
View Solution
