Compute the area of the loop of the curvey2=x2[1+x1–x].
Text Solution
The correct Answer is:2−(π/2) sq. units
|
Topper's Solved these Questions
- AREA UNDER THE CURVEBOOK - MOTIONCHAPTER - AREA UNDER THE CURVEEXERCISE - EXERCISE - 4 LEVEL - I
11 Videos
- AREA UNDER THE CURVEBOOK - MOTIONCHAPTER - AREA UNDER THE CURVEEXERCISE - EXERCISE - 4 LEVEL - II
14 Videos
- AREA UNDER THE CURVEBOOK - MOTIONCHAPTER - AREA UNDER THE CURVEEXERCISE - EXERCISE - 2 (LEVEL-II)
4 Videos
- BASIC MATHEMATIC & LOGARITHM BOOK - MOTIONCHAPTER - BASIC MATHEMATIC & LOGARITHM EXERCISE - Exercise - 4
4 Videos
Similar Questions
Knowledge Check
The area bounded by the loop of the curve y2=x2(1−x) is
A25sq.unitsB85sq.unitsC215sq.unitsD815sq.units
Compute the area enclosed by the loop of the curve y2=x(x−1)2
View SolutionCompute the area enclosed by the curve y2=(1−x2)3
View SolutionShow that the area of the loop of the curve y2=x2(1−x) is 815.
View SolutionCompute the area of the figure enclosed by the curve y2=x2(1−x2)
View SolutionCompute the area enclosed by the loop of the curve 4(y2−x2)+x3=0
View SolutionCompute the area enclosed by the loop of the curve x3+x2−y2=0
View SolutionFind the area enclosed by the loop of the curve y2=(x−1)(x−2)2.
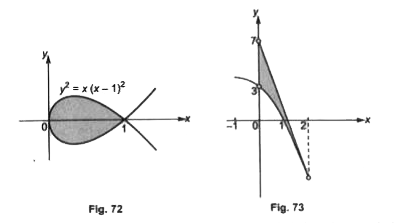
View Solution
