Let $C_{1} and C_{2}$ be two curves passing through the origin as shown in the figure. A curve C is said to ‘‘bisect the area’’ the region between $C_{1} and C_{2}$ , if for each point P of C, the two shaded regions A and B shown in the figure have equal areas. Determine the upper curve $C_{2}$ , given that the bisecting curve C has the equation $y = x^{2}$ and that the lower curve $C_{1}$ has the equation $y = x^{2} / 2 .$

Video Solution

Text Solution

Verified by Experts

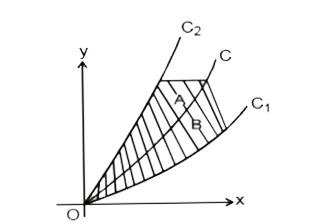
The correct Answer is: $(\frac{16}{9}) x^{2}$

Updated on:21/07/2023

Answer

Step by step video & image solution for Let C_(1 )and C_(2) be two curves passing through the origin as shown in the figure. A curve C is said to ‘‘bisect the area’’ the region between C_(1) and C_(2), if for each point P of C, the two shaded regions A and B shown in the figure have equal areas. Determine the upper curve C_(2), given that the bisecting curve C has the equationy = x^(2) and that the lower curve C_(1) has the equation y = x^(2)//2. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Knowledge Check

If the curve $y = a x^{2} + b x + c$ passes through the point (1, 2) and the line y = x touches it at the origin, then
Aa = 1, b = -1, c = 0
Ba = 1, b = 1, c = 0
Ca = -1, b = 1, c = 0
Dnone of these
In the following figure, four curves A,B, C and D are shown. The curves are

AIsothermal for A and D while adiabatic for B and C
BAdiabatic for A and C while isothermal for B and D
CIsothermal for A and B while adiabatic for C and D
DIsothermal for A and C while adiabatic for B and D
The area of the region bounded by the curve C $: y = \frac{x + 1}{x^{2} + 1}$ nad the line y=1 , is
Aml $- \frac{1}{2} In 2 + \frac{π}{4}$
B $In 2 - \frac{π}{4} + 1$
C $\frac{1}{2} In 2 + \frac{π}{4} - 1$
DIn $2 - \frac{π}{2} + 1$