Four identical spheres each of radius 10 cm and mass 1 kg are placed on a horizontal surface touching one another so that their centres are located at the corners of square of side 20 cm. What is the distance of their centre of mass from centre of either sphere ?
5 cm
10 cm
20 cm
None of these
The correct Answer is:D
To find the distance of the center of mass of four identical spheres from the center of either sphere, we can follow these steps:
1. Understanding the Configuration:
- We have four identical spheres, each with a radius of 10 cm and a mass of 1 kg.
- The spheres are placed such that their centers form the corners of a square with a side length of 20 cm.
2. Identifying the Centers of the Spheres:
- The centers of the spheres are at the corners of the square. Let's denote the corners as A, B, C, and D.
- The coordinates of the centers can be assigned as follows:
- A (0, 0)
- B (20, 0)
- C (20, 20)
- D (0, 20)
3. Calculating the Center of Mass:
- The formula for the center of mass (CM) of a system of particles is given by:
CM=∑mi⋅ri∑mi
- Here, mi is the mass of each sphere (1 kg) and ri are the position vectors of the centers.
4. Calculating the x-coordinate of CM:
- The x-coordinates of the centers are 0, 20, 20, and 0.
- Therefore, the x-coordinate of the center of mass is:
xCM=1⋅0+1⋅20+1⋅20+1⋅01+1+1+1=404=10 cm
5. Calculating the y-coordinate of CM:
- The y-coordinates of the centers are 0, 0, 20, and 20.
- Therefore, the y-coordinate of the center of mass is:
yCM=1⋅0+1⋅0+1⋅20+1⋅201+1+1+1=404=10 cm
6. Finding the Distance from the Center of Either Sphere:
- The center of any sphere (for example, sphere A) is at (0, 0).
- The center of mass is at (10, 10).
- The distance d from the center of sphere A to the center of mass is calculated using the distance formula:
d=√(xCM−xA)2+(yCM−yA)2=√(10−0)2+(10−0)2=√100+100=√200=10√2 cm
Final Answer:
The distance of the center of mass from the center of either sphere is 10√2 cm.
- We have four identical spheres, each with a radius of 10 cm and a mass of 1 kg.
- The spheres are placed such that their centers form the corners of a square with a side length of 20 cm.
- The centers of the spheres are at the corners of the square. Let's denote the corners as A, B, C, and D.
- The coordinates of the centers can be assigned as follows:
- A (0, 0)
- B (20, 0)
- C (20, 20)
- D (0, 20)
- The formula for the center of mass (CM) of a system of particles is given by:
CM=∑mi⋅ri∑mi
- Here, mi is the mass of each sphere (1 kg) and ri are the position vectors of the centers.
- The x-coordinates of the centers are 0, 20, 20, and 0.
- Therefore, the x-coordinate of the center of mass is:
xCM=1⋅0+1⋅20+1⋅20+1⋅01+1+1+1=404=10 cm
- The y-coordinates of the centers are 0, 0, 20, and 20.
- Therefore, the y-coordinate of the center of mass is:
yCM=1⋅0+1⋅0+1⋅20+1⋅201+1+1+1=404=10 cm
- The center of any sphere (for example, sphere A) is at (0, 0).
- The center of mass is at (10, 10).
- The distance d from the center of sphere A to the center of mass is calculated using the distance formula:
d=√(xCM−xA)2+(yCM−yA)2=√(10−0)2+(10−0)2=√100+100=√200=10√2 cm
The distance of the center of mass from the center of either sphere is 10√2 cm.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-I)40videos
CENTRE OF MASS
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-II)28videos
CENTRE OF MASS
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II20videos
CENTRE OF MASS
- BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II19videos
Capacitance
- BOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 416videos
CIRCULAR MOTION
Similar Questions
Three identical spheres each of radius 3cm are placed on a horizontal surface touching one another. The distance of centre of mass of system from any centre of the sphere is
View SolutionThree identical spheres each of radius 'R' are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is.
View Solution
Knowledge Check
- Question 1 - Select One
Two identical spheres of radius 2 cm and mass 1 kg are placed 1 cm apart on the surface of the earth. Then,
Athe two spheres move towards each other.Bthe two spheres move away from each other.Cthere is no force of attraction between the two spheres.DNone of these - Question 2 - Select One
Three identical balls each of radius 10 cm and mass 1 kg each are placed touching one another on a horizontal surface. Where is their centre of mass located?
AOn the horizontal surfaceBAt the point of contact of any two spheresCAt the centre of one ballDnone of these - Question 3 - Select One
Three identical particles each of mass 0.1kg are arranged at three corners of a square of side √2m. The distance of the centre of mass from the fourth corners is
A2/3mB4/3mC1mD8/3m
Four point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.
 View Solution
View SolutionThree identical spheres, each of mass 1 kg are kept as shown in figure, touching each other, with their centres on a straight line. If their centres are marked P, Q, R respectively, the distance of centre of mass of the system from P (origin) is
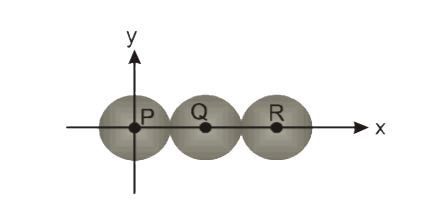 View Solution
View SolutionFour particles of masses m, m, 2m and 2m are placed at the corners of a square of side a, as shown in fig. Locate the centre of mass.
View SolutionThree identical spheres each of mass m and radius R are placed touching each other so that their centres A,B and C lie on a straight line. The position of their centre of mass from centre of A is
View SolutionConsider a system of two spheres of masses 5 kg and 25 kg. The distance between their centres is 1.2 m. What is the distance of their centre of mass from the centre of the sphere of mass 5 g?
View Solution
