In the figure shown the block A collides head on with another block B at rest. Mass of B is twice the mass of A. The block A stops after collision. The co-efficient of restitution is :
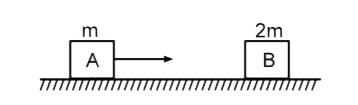
0.5
1
0.25
it is not possible
The correct Answer is:A
Step by step video & image solution for In the figure shown the block A collides head on with another block B at rest. Mass of B is twice the mass of A. The block A stops after collision. The co-efficient of restitution is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-I)
40 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-II)
28 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II
20 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II
19 Videos
- CIRCULAR MOTIONBOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 4
16 Videos
Similar Questions
A block of mass m moving at speed υ collides wilth another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View Solution(i) A block of mass m moving towards right with a velocity V strikes (head on) another block of mass M which is at rest connected to a spring. The coefficient of restitution for collision between the blocks is e = 0.5.
Find the ratio Mm for which the subsequent compression in the spring is maximum. There is not friction.

Ball A collides head on with another identical ball B at rest. Find the coefficient of restitution if ball B has 80% of the total kinetic energy of the system after collision.
View Solution
Knowledge Check
A ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
A(a) 12B(b) 23C(c) 14D(d) None of theseA particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
A1BmMCM−mM+mDmM+mA block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
A8 JB4×10−7JC4 JD0 J
A block of mass 5 kg moves from left to right with a velocity of 2ms−1 and collides with another block of mass 3 kg moving along the same line in the opposite direction with velocity 4ms−1.
(i) If the collision is perfectly elastic, determine velocities of both the blocks after their collision.
(ii) If coefficient of restitution is 0.6, determine velocities of both the blocks after their collision.
View SolutionIn the figure shown, the block A of mass m collides with the identical block B and after collision they stick together. Calculate the amplitude of resulatant vibration.
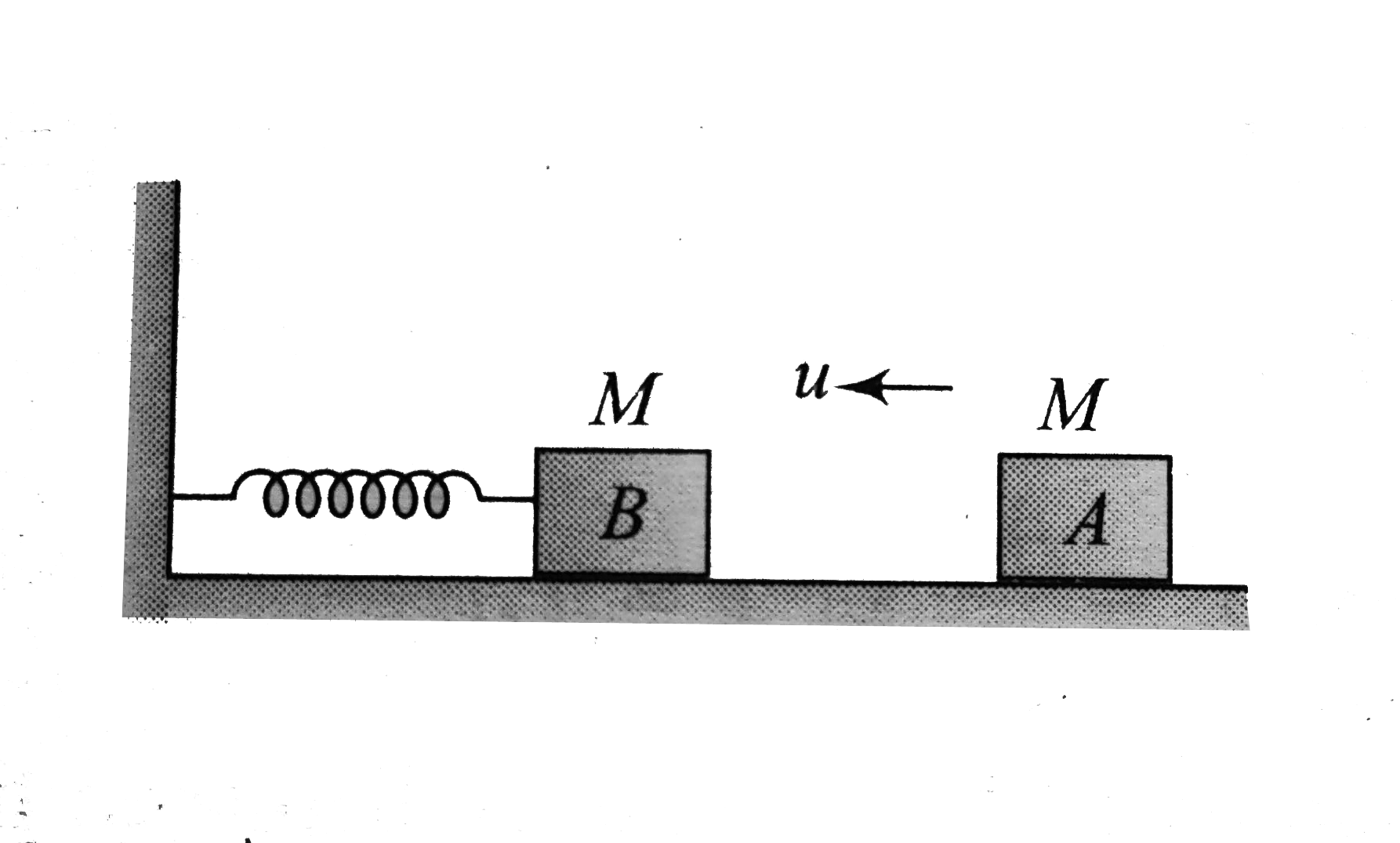
View SolutionIn the arrangement shown in Fig. the ball and the block have the same mass m=1kg each, θ=60∘ and length l=2.50m. Coefficient of friction between the block and the floor is 0.5. When the ball is released from the position shown in Fig. it collides with the block and the block stops after moving a distance 2.50m.
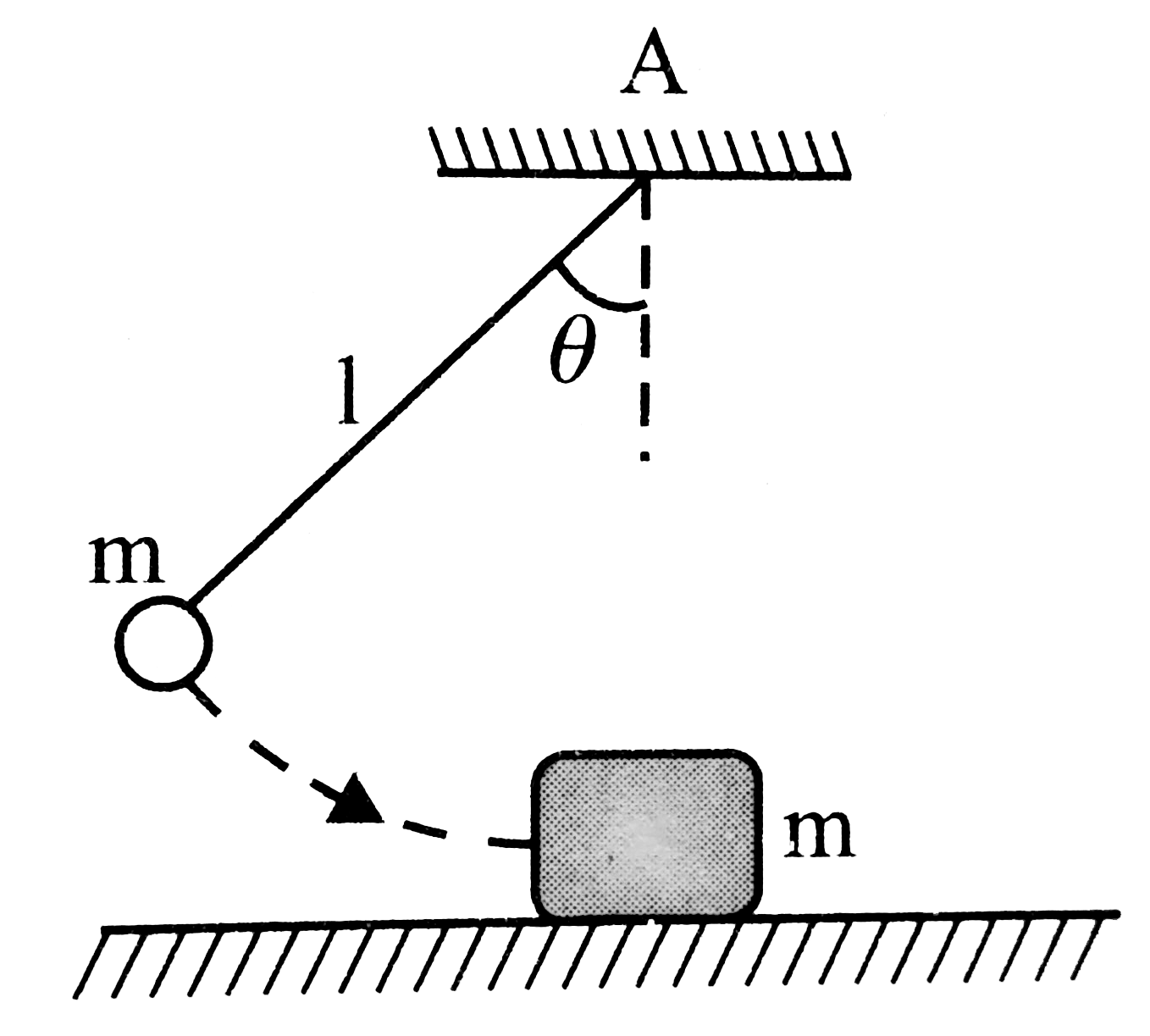
The coefficient of restitution for collision between the ball and the block is
View SolutionTwo block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.
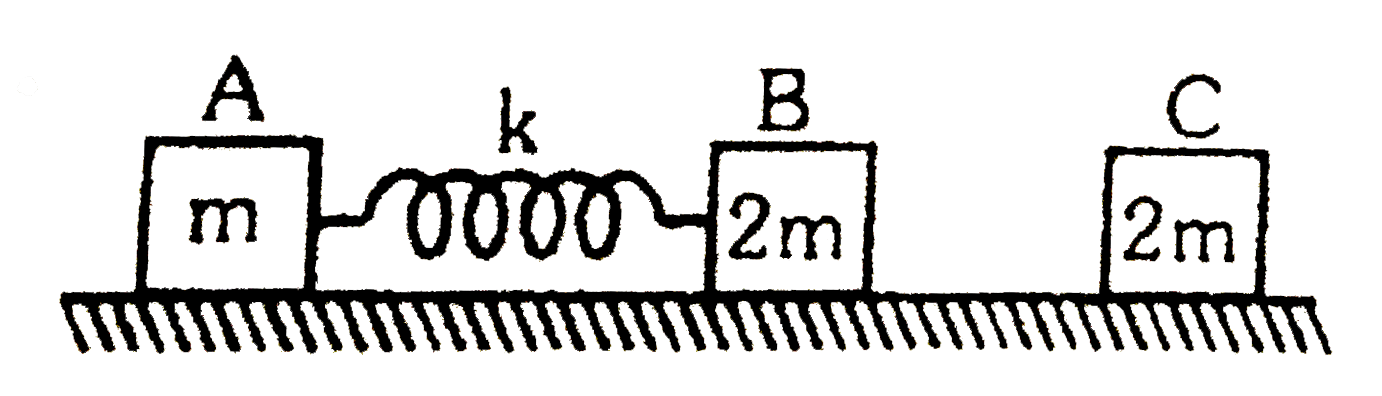
The velocity of block B just after collision is -
View SolutionA block having mass m collides with an another stationary block having mass 2m. The lighter block comes to rest after collision. If the velocity of first block is v, then the value is coefficient of restitution will must be
View Solution
