A bullet of mass m = 50 gm strikes a sand bag of mass M = 5 kg hanging from a fixed point, with a horizontal velocity →vp . If bullet sticks to the sand bag then the ratio of final & initial kinetic energy of the bullet is (approximately) :
10−2
10−3
10−6
10−4
The correct Answer is:D
To solve the problem, we need to find the ratio of the final kinetic energy to the initial kinetic energy of the bullet after it strikes the sandbag and sticks to it. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Problem
We have a bullet of mass m=50g=0.05kg and a sandbag of mass M=5kg. The bullet strikes the sandbag with a horizontal velocity →vp. After the collision, the bullet sticks to the sandbag.
Step 2: Apply Conservation of Momentum
Since the bullet sticks to the sandbag, we can use the conservation of momentum in the horizontal direction. The initial momentum of the system (bullet + sandbag) before the collision is equal to the final momentum after the collision.
Initial Momentum:
pinitial=m⋅vp
Final Momentum:
After the collision, the bullet and the sandbag move together with a common velocity v:
pfinal=(m+M)⋅v
Setting the initial momentum equal to the final momentum:
m⋅vp=(m+M)⋅v
Step 3: Substitute Known Values
Substituting the values:
0.05⋅vp=(0.05+5)⋅v
0.05⋅vp=5.05⋅v
Step 4: Solve for Final Velocity v
Rearranging the equation to solve for v:
v=0.05⋅vp5.05
Step 5: Calculate the Ratio of Kinetic Energies
The initial kinetic energy of the bullet is given by:
KEinitial=12mv2p
The final kinetic energy of the bullet and sandbag system is:
KEfinal=12(m+M)v2
Step 6: Substitute v into Final Kinetic Energy
Substituting v into the final kinetic energy expression:
KEfinal=12(5.05)(0.05⋅vp5.05)2
=12(5.05)⋅0.0025⋅v2p(5.05)2
=0.00252⋅5.05v2p
Step 7: Find the Ratio of Final to Initial Kinetic Energy
Now, we can find the ratio:
KEfinalKEinitial=0.00252⋅5.05v2p12⋅0.05v2p
The v2p and 12 cancel out:
=0.00250.05⋅5.05
=0.00250.2525≈0.00988
Step 8: Final Calculation
To find the approximate ratio:
KEfinalKEinitial≈10−4
Conclusion
Thus, the ratio of the final kinetic energy to the initial kinetic energy of the bullet is approximately 10−4.
We have a bullet of mass m=50g=0.05kg and a sandbag of mass M=5kg. The bullet strikes the sandbag with a horizontal velocity →vp. After the collision, the bullet sticks to the sandbag.
Since the bullet sticks to the sandbag, we can use the conservation of momentum in the horizontal direction. The initial momentum of the system (bullet + sandbag) before the collision is equal to the final momentum after the collision.
pinitial=m⋅vp
After the collision, the bullet and the sandbag move together with a common velocity v:
pfinal=(m+M)⋅v
m⋅vp=(m+M)⋅v
Substituting the values:
0.05⋅vp=(0.05+5)⋅v
0.05⋅vp=5.05⋅v
Rearranging the equation to solve for v:
v=0.05⋅vp5.05
The initial kinetic energy of the bullet is given by:
KEinitial=12mv2p
KEfinal=12(m+M)v2
Substituting v into the final kinetic energy expression:
KEfinal=12(5.05)(0.05⋅vp5.05)2
=12(5.05)⋅0.0025⋅v2p(5.05)2
=0.00252⋅5.05v2p
Now, we can find the ratio:
KEfinalKEinitial=0.00252⋅5.05v2p12⋅0.05v2p
The v2p and 12 cancel out:
=0.00250.05⋅5.05
=0.00250.2525≈0.00988
To find the approximate ratio:
KEfinalKEinitial≈10−4
Thus, the ratio of the final kinetic energy to the initial kinetic energy of the bullet is approximately 10−4.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-I)
40 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-II)
28 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II
20 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II
19 Videos
- CIRCULAR MOTIONBOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 4
16 Videos
Similar Questions
A bullet of mass m=10 gm strikes a hanging block of mass M=50 gm inelastically, with a horizontal velocity v0=60m/s. Find the change in tension (in N) in the string during collision. Round of to nearest integer. (Take : l=1m)
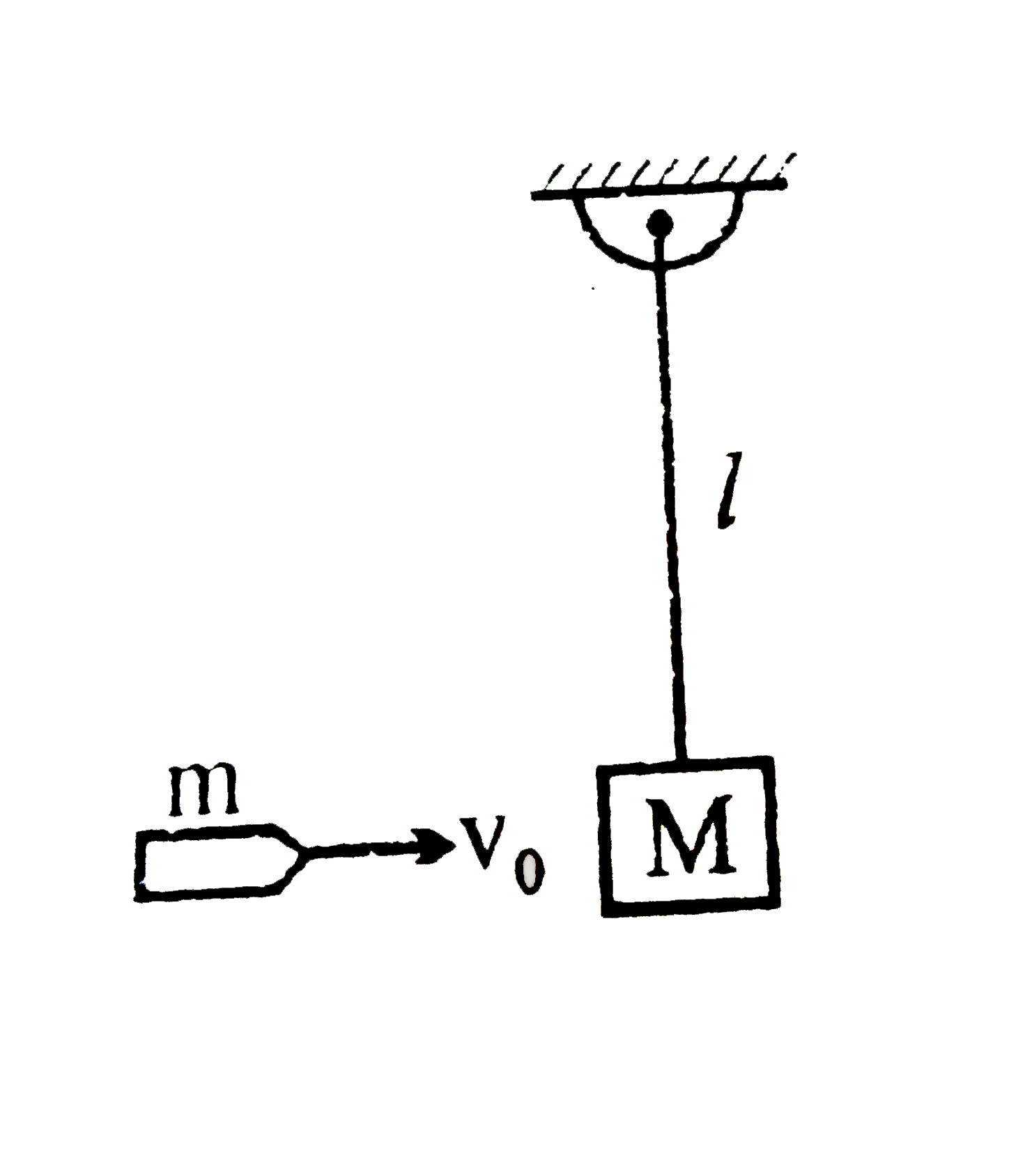
View SolutionA bullet of mass 5 g travels with a speed of 500m/s. If it penetrates a fixed target which offers a constant resistive force of 1000N to the motion of the bullet, find (a) the initial kinetic energy of the bullet (b) the distance through which the bullet has penetrated.
View Solution
Knowledge Check
A bullet of mass m=50 gm strikes (Δt≈0)a sand bag of mass M =5 kg hanging from a fixed point, with a horizontal velocity →vp. If bullet sticks to the sand bag then the ratio of final & initial kinetic energy of the bullet is
A10−2B10−3C10−6D10−4A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2A bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 A√2ghBM+mm√ghCmM+m2ghDM+mM√2gh
A√2ghBM+mm√ghCmM+m2ghDM+mM√2gh
A bullet of mass 50 g is fired from a gun with initial velocity of 35 m/s. If mass of the gun is 4 kg, then calculate the recoil velocity of the gun.
View SolutionA bullet of mass 50 g is fired from a gun with initial velocity of 35 m/s . If mass of the gun is 4 kg , then calculate the recoil velocity of the gun .
View SolutionA bullet of mass 10 g is fired from a gun of mass 1 kg with recoil velocity of gun 5 m/s. The muzzle velocity will be
View SolutionA bullet of mass 10gm strikes a target at 400m/s velocity and does half of its initial velocity. The loss of kinetic energy in joules is
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View Solution
