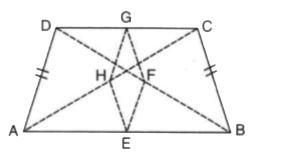
ABCD is a quadrilateral and its diagonals intersect at O.E,F,GandH are the midpoints of AO,BO,CO,andDO respectively. If the area of EFGH=50cm2, find the area of ABCD.
Step by step video & image solution for ABCD is a quadrilateral and its diagonals intersect at O. E,F,G and H are the midpoints of AO, BO, CO, and DO respectively. If the area of EFGH = 50cm^2, find the area of ABCD. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
ABCD is a parallelogram in which diagonals AC and BD intereset at O. If E, F, G and H are the mid points of AO, DO, CO and BO respectively, then the ratio of the perimeter of the quadrilateral EFGH to the perimeter of parallelogram ABCD is:
A1:4B2:3C1:2D1:3ABCD is a parallelogram in which diagonals AC and BD intereset at O. If E, F, G and H are the mid points of AO, DO, CO and BO respectively, then the ratio of the perimeter of the quadrilateral EFGH to the perimeter of parallelogram ABCD is:
A0.042361111111111B0.043055555555556C0.04375D0.044444444444444ABCD is a parallelogram. The diagonals AC and BD intersect at a point O. If E,F,GandH are the mid-points of AO,DO,COandBO respectively, then the ratio of (EF+FG+GH+HE) to (AD+DC+CB+BA) is:
A1:1B1:2C1:3D1:4
Let ABCD be a parallelogram of area 124cm2. If E and F are the mid-points of sides AB and CD respectively, then find the area of parallelogram AEFD.
View SolutionLet ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and CD respectively, then find the area of parallelogram AEFD
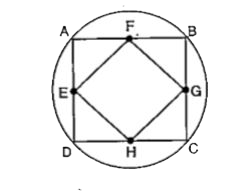
View SolutionABCD is a square inscribed in a circle of radius 14 cm, E,F,G and H are the midpoints of the sides DA, AB, BC and CD respectively. The area of the square EFGH will be
View SolutionABCD is a quadrilateral. The diagonals of ABCD intersect at the point P. The area of the triangles APD and BPC are 27 and 12, respectively. If the areas of the triangles APB and CPD are equal, then the area of triangle APB is
View SolutionIn an equilateral triangle ABC, AO, BO and CO are the angle bisectors meet at the incentre 'O'.D, E and F are the mid- points of AO, BO and CO respectively. A circle with centre 'O' passes through D, E and F. Area of the circle is 3πcm2. What is the perimeter of triangles (Δ)ABC?
View Solution