ABCD एक समान्तर चतुर्भुज है जिसकी भुजाओं AB, BC, CD और DA के क्रमशः E, F, G और H मध्यबिंदु है। दर्शाए कि
चतुर्भुज EFGH का क्षेत्रफल (चतुर्भुज ABCD का क्षेत्रफल )
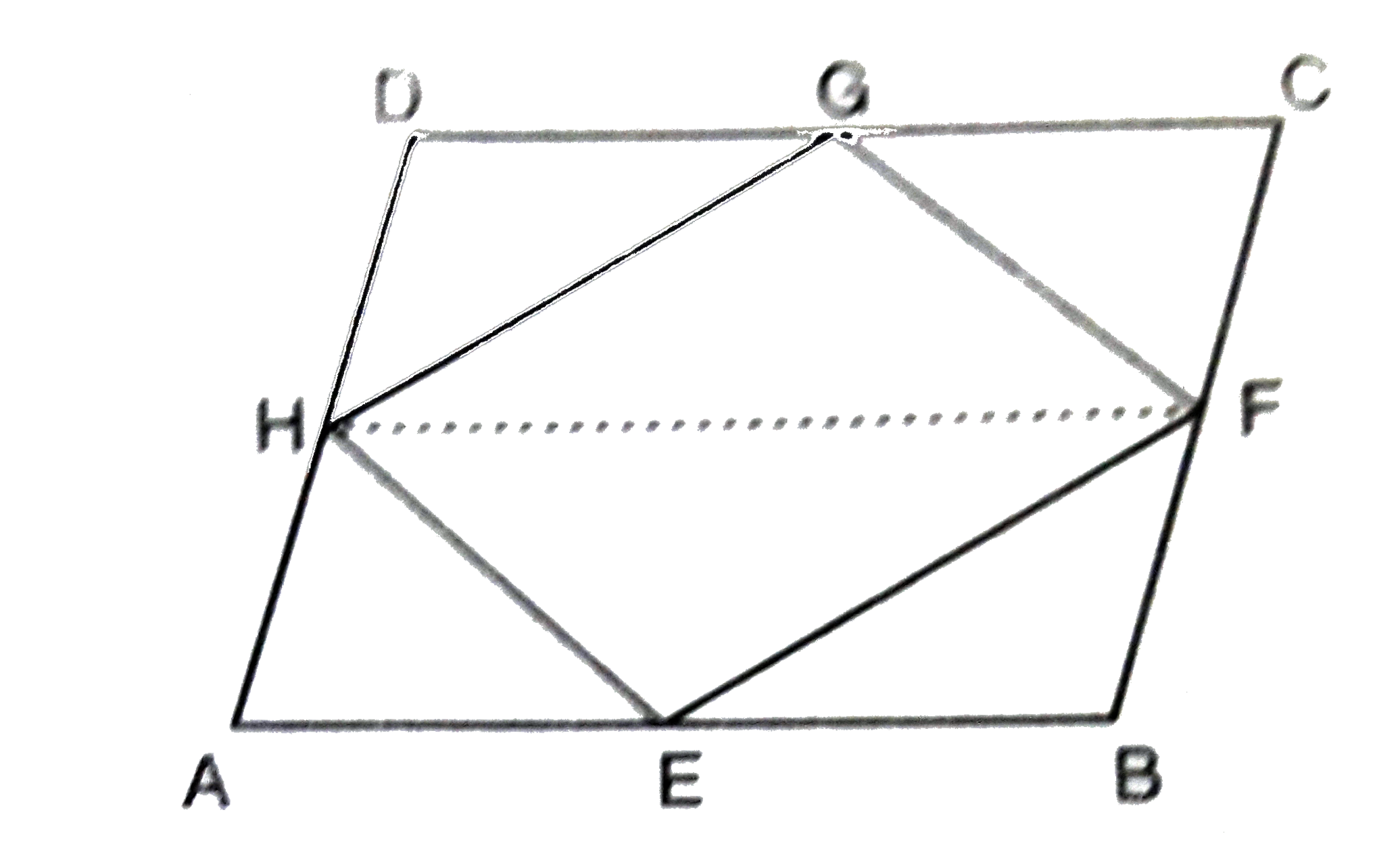
HF को मिलाइए
चूँकि H और F क्रमशः AD और BC के मध्यबिंदु है।
तथा
चूँकि ABCD एक समान्तर चतुर्भुज है।
तथा AD ।। BC
तथा AD ।। BC
तथा AH ।। BF
ABFH एक समान्तर चतुर्भुज है।
चूँकि समान्तर चतुर्भुज FHAB तथा एक ही आधार FH तथा एक ही समान्तर रेखाओं HF और AB के बीच स्थित हैं।
का क्षेत्रफल (समान्तर चतुर्भुज FHAB का क्षेत्रफल ) ...(i)
इसी प्रकार, यह दर्शा सकते है कि
का क्षेत्रफल ( समान्तर चतुर्भुज FHDC का क्षेत्रफल ) ...(ii)
(i) और (ii ) को संगत पक्षों को जोड़ने पर
का क्षेत्रफल का क्षेत्रफल
( समान्तर चतुर्भुज FHAB का क्षेत्रफल ) (समान्तर चतुर्भुज FHDC का क्षेत्रफल )
का क्षेत्रफल { ( समान्तर चतुर्भुज FHAB का क्षेत्रफल ) + ( समान्तर चतुर्भुज FHDC का क्षेत्रफल ) }
का क्षेत्रफल (समान्तर चतुर्भुज ABCD का क्षेत्रफल )
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - व्याख्यात्मक उदाहरण
1 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.1
6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionसामान्य चतुर्भुज का क्षेत्रफल |विशेष चतुर्भुजों का क्षेत्रफल
View SolutionRevision|हीरोन के सूत्र पर आधारित महत्वपूर्ण प्रश्न#!#त्रिभुज का क्षेत्रफल तथा चतुर्भुज का क्षेत्रफल
View SolutionRevision|चतुर्भुज#!#चतुर्भुज के प्रकार#!#समान्तर चतुर्भुज
View Solutionहीरोन का सूत्र|चतुर्भुज का क्षेत्रफल#!#महत्वपूर्ण प्रश्नो पर चर्चा
View Solutionहीरोन का सूत्र|चतुर्भुज का क्षेत्रफल#!#महत्वपूर्ण प्रश्न
View Solutionहीरोन का सूत्र|त्रिभुज का क्षेत्रफल#!#चतुर्भुज का क्षेत्रफल#!#महत्वपूर्ण प्रश्न
View Solutionहीरोन का सूत्र|चतुर्भुज का क्षेत्रफल#!#महत्वपूर्ण प्रश्न
View Solutionहीरोन का सूत्र|त्रिभुज का क्षेत्रफल#!#चतुर्भुज का क्षेत्रफल#!#महत्वपूर्ण प्रश्न
View SolutionABCD is a trapezium with AD and BC parallel sides. E is a point on BC. The ratio of the area trapezium ABCD to that of triangle AED is- ABCD एक AD और BC समांतर भुजाओं वाला समलंब चतुर्भुज है। E,BC पर एक बिंदु है। square ABCD और triangle AED के क्षेत्रफल का अनुपात क्या होगा?
View SolutionABCD is a quadrilateral such that angle D= 90^@ . A circle with centre O touches the sides AB, BC and CD and DA at P, Q, R and S respectively. If BC = 40 cm, BP = 28 cm and CD = 25 cm, then what is the radius of the circle is: ABCD एक चतुर्भुज है जैसे angle D= 90^@ । केन्द्र O वाला एक वृत्त क्रमशः AB, BC और CD और DA को P, Q,R और S से छूता है। यदि BC = 40 सेमी, BP = 28 सेमी और CD = 25 सेमी है, तो वृत्त का त्रिज्या क्या है
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=158∘. Then ∠BAC is equal to :
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इसे घेरने वाले वृत्त का व्यास है और ∠ADC=158∘ है | कोण BAC का मान ज्ञात करें |
View Solution
