Doubtnut Promotions Sticky

E is the mid-point of the diagonal AC of the rectangle ABCD; if the coordinates of A and E are (7,−8)and(2,−2), then state which of the following are the coordinates of C?

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for E is the mid-point of the diagonal AC of the rectangle ABCD; if the coordinates of A and E are (7,-8) and (2, -2), then state which of the following are the coordinates of C? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSDEFAULT

Similar Questions

Knowledge Check

  • Question 1 - Select One

    ocr_image
    In the xy-plane above, ABCD is a square and point E is the center of the square. The coordinates of points C and E are (7, 2) and (1, 0), respectively. Which of the following is an equation of the line that passes through points B and D ?

    Ay=−3x−1
    By=−3(x−1)
    Cy=−13x+4
    Dy=−13x−1
  • Question 2 - Select One

    E and F are mid-points of diagonals AC and BD of □ABCD. If G is the mid-point of seg EF, then

    A4 ¯¯¯¯¯¯AG
    B¯0
    C0
    D2¯¯¯¯¯¯GC
  • Question 3 - Select One

    As shown below, the diagonals of rectange EFGH intersect at the point (-2,-4) in the standard (x,y) coordinate plane. Point F is at (-7,-2) . Which of the following are the coordinates of H ?
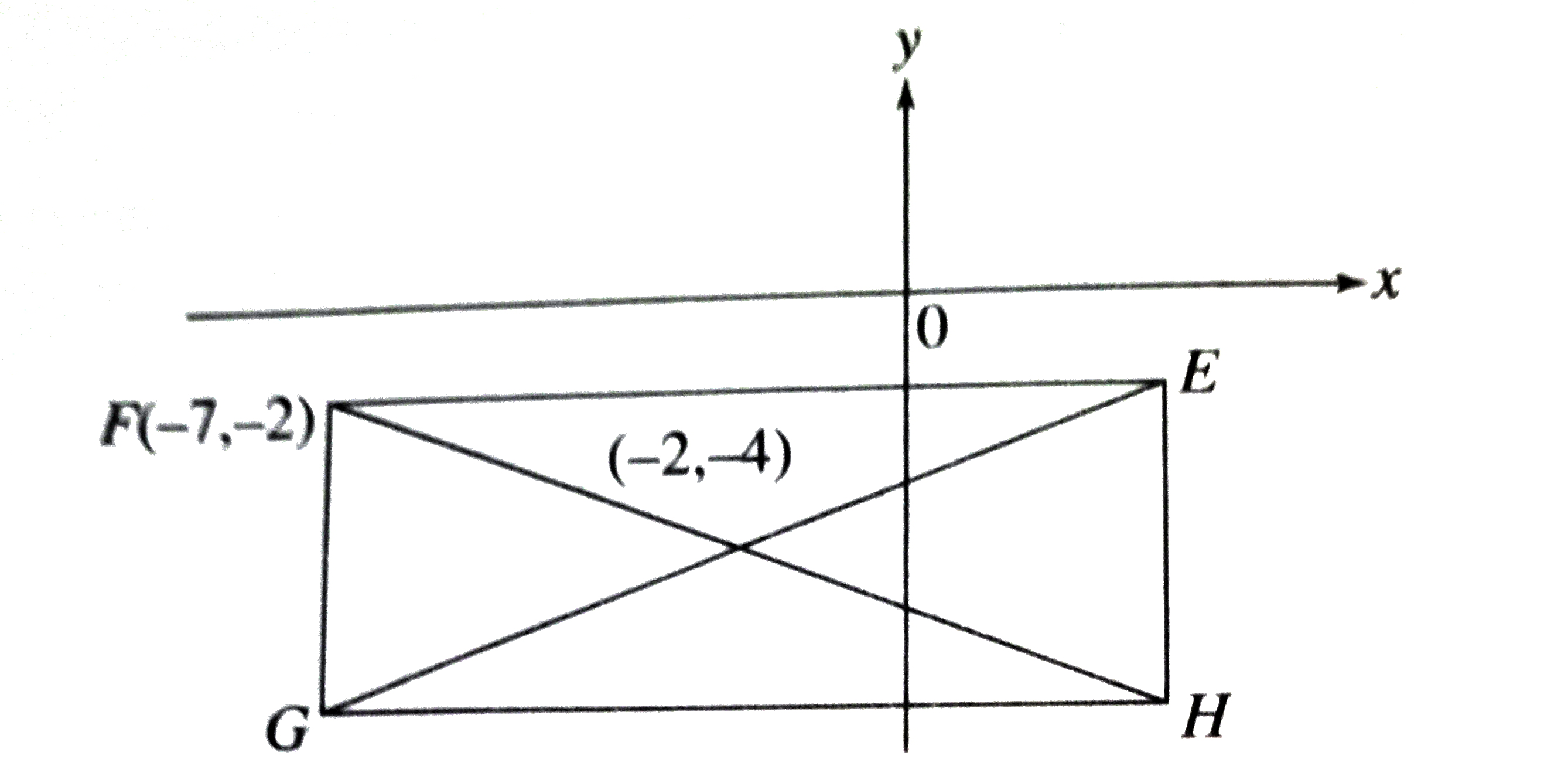    ocr_image

    A(−412,−3)
    B(-7, -6)
    C(3,-2)
    D(3,-6)