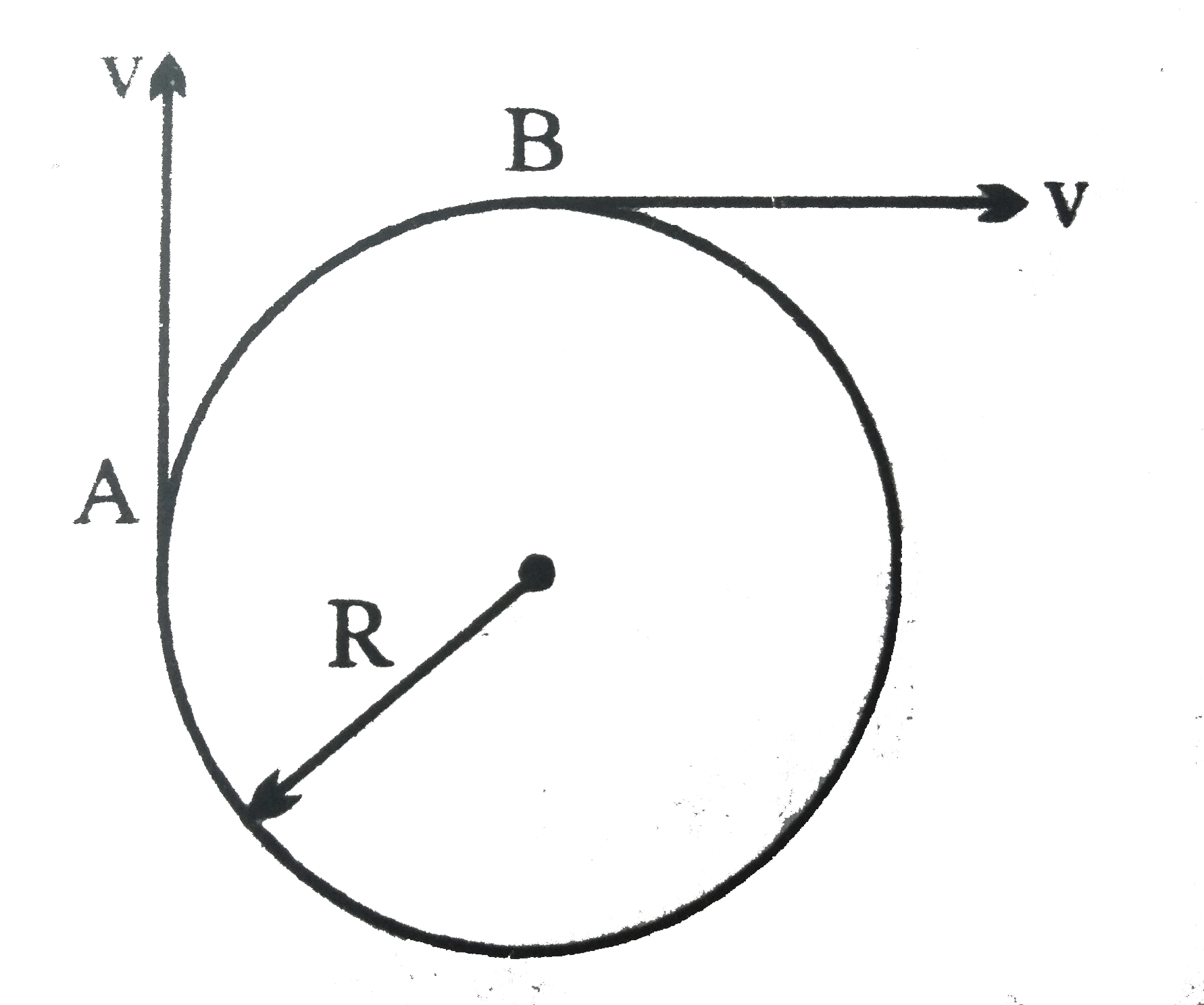
Consider a rigid body rotating in a plane. We wish to determine the angular velocity of the rigid body given the known velocities of points A and B on the rigid body. These velocities are parallel and pointing in the same direction. The line joining points A and B is perpendicular to the direction of the velocities. The figure below illustrates the set up of the problem.
Note that lC is the intersection of the line passing through points A and B, and the line joining the tip of the vectors vAandvB

vB−vAd
vB+vAd
vB−vA2d
none of these
The correct Answer is:A
Step by step video & image solution for Consider a rigid body rotating in a plane. We wish to determine the angular velocity of the rigid body given the known velocities of points A and B on the rigid body. These velocities are parallel and pointing in the same direction. The line joining points A and B is perpendicular to the direction of the velocities. The figure below illustrates the set up of the problem. Note that lC is the intersection of the line passing through points A and B, and the line joining the tip of the vectors v_(A) and v_(B) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 2 (Level - II)
Explore 25 Videos
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 3 (Level - I)
Explore 27 Videos
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 1
Explore 77 Videos
- ALTERNATING CURRENTBook:MOTIONChapter:ALTERNATING CURRENTExercise:EXERCISE - 4 (LEVEL - II)
Explore 14 Videos
Similar Questions
Knowledge Check
The angular momentum of a rigid body is
Athe moment of the acting force.Bmoment of the momentum.Cmoment of the mass.Dmoment of the acceleration.The angular velocity of a rigid body about any point of that body is same :
Aonly in magnitudeBonly in directionCboth in magnitude and direction necessarilyDboth in magnitude and direction about some points but not about all points.If the angular velocity of a rotating rigid body is increased then its moment of inertia about that axis
AincreasesBdecreasesCbecomes zeroDremains unchanged
The angular velocity of a rigid body is 24 rad s−1, Calculate the time it will take to rotate 72 rad.
View SolutionA rigid body of mass m rotates about an axis passing through its centre. If the angular velocity of the body is unity, the moment of inertia of the body will be equal to
View SolutionA rigid body of mass m rotates about an axis passing through its centre. If the angular velocity of the body is unity, the moment of inertia of the body will be equal to
View SolutionTwo points of a rigid body are moving as shown. The angular velocity of the body is :
 .
.
View SolutionIf the velocity of centre of mass of a rolling body is V then velocity of highest point of that body is
View Solution