Four point masses are fastened to the corners of a frame of negligible mass lying in the xy plane. Let w be the angular speed of rotation. Then
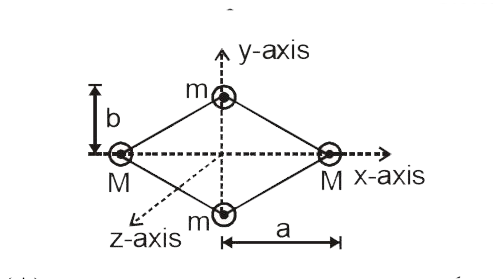
rotational kinetic energy associated with a given angular speed depends on the axis of rotation.
rotational kinetic energy about y-axis is independent of m and its value is Ma2ω2
rotational kinetic energy about z-axis depends on m and its value is (Ma2+mb2)ω2
rotational kinetic energy about z-axis is independent of m and its value is Mb2ω2
The correct Answer is:A, B, C
Step by step video & image solution for Four point masses are fastened to the corners of a frame of negligible mass lying in the xy plane. Let w be the angular speed of rotation. Then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 3 (Level - I)
27 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 3 (Level - II)
20 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 2 (Level -I)
51 Videos
- ALTERNATING CURRENTBOOK - MOTIONCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - 4 (LEVEL - II)
14 Videos
Similar Questions
Four point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View SolutionFour point masses, each of mass m, are fixed at the corners of a square of side l. The square is rotating with angular frequency ω, about an axis passing through one of the corners of the square and parallel to its diagonal , as shown, Angular momentum about this axis is :

View Solution
Knowledge Check
Four small objects each of mass m are fixed at the corners of a rectangular wire-frame of negligible mass and of sides a and b (a > b) . If the wire frame is now rotated about an axis passing along the side of length then the moment of inertia of the system for this axis of rotation is:
A2ma2B4ma2C2m(a2+b2)D2m(a2−b2)Four small objects each of mass m are fixed at the corners of a rectangular wire-frame of negligible mass and of sides a and b (a > b). If the wire frame is now rotated about an axis passing along the side of length b, then the moment of inertia of the system for this axis of rotation is
A2ma2B4ma2C2m(a2+b2)D2m(a2−b2)Four particles, each of mass 1kg are placed at the corners of a square of side 1m in the XY plane. If the point of intersecting of the diagonals of the square is taken as the origin, the co-ordinates fo the centre of mass are
A(1,1)B(−1,1)C(1,−1)D(0,0)
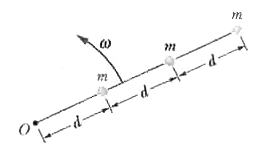
In Figure, three particles of mass m = 23 g are fastened to three rods of length d = 12 cm and negligible mass. The rigid assembly rotates around point O at the angular speed ω=0.85rad/s. About O, what are (a) the rotational inertia of the assembly, (b) the magnitude of the angular momentum of the middle particle, and ( c) the magnitude of the angular momentum of the assembly?
View SolutionFour small objects each of mass m are fixed at the comers of a rectangular wire-frame of negligible mass and of sides a and b(a>b). If the wire frame is now rotated about an axis passing along the side of length b, then the moment of inertia of the system for this axis of rotation is
View SolutionFour particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system the moment of inertia of four bodies about an axis perpendicular to the plane of frame and passing through a corner is
View SolutionFour point size bodies each of mass m are fixed at four corners of light square frame of side length 1m. The radius of gyration of these four bodies about an axis perpendicular to the plane of frame passing through its centre is
View SolutionFour particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system the moment of inertia of four bodies about an axis passing through opposite corners of frame is
View Solution
