A ring of mass M and radius R is rotating with angular speed ω about a fixed vertical axis passing through its centre O with two point masses each of mass M8 at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is 89ω and one fo the masses is at a distance of 35R from O. At this instant the distance of the other mass from O is
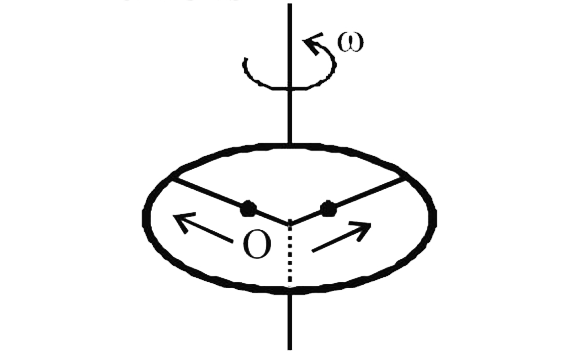
23R
13R
35R
45R
The correct Answer is:D
Step by step video & image solution for A ring of mass M and radius R is rotating with angular speed omega about a fixed vertical axis passing through its centre O with two point masses each of mass (M)/(8) at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is (8)/(9) omega and one fo the masses is at a distance of (3)/(5) R from O. At this instant the distance of the other mass from O is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2A uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity ω . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be
A(M−2m)ω(M−m)B(M+2m)ω(M+m)C(M−2m)ω(M+m)D(M+2m)ω(M−m)A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
A12mr2ω2Bmrω2Cmr2ω2D12mrω2
A uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
View SolutionA smoothh disc is rotating with uniform angular speed ω about a fixed vertical axis passing through its centre and normal to its plane as shown. A small block of mass m is gently placed at the periphery of the disc. Then (pickup the correct alternative or alternatives)

View SolutionA thin circular ring of mass per unit length p and radius r is rotating at an angular speed ω as shown in figure. The tension in the ring is

View SolutionA uniform disc of radius 'a' and mass 'm' is rotating freely with angular speed ω in a horizontal plane about a smooth fixed vertical axis through its centre. A particle of mass 'm' is then suddenly attached to the rim of the disc and rotates with it. The new angular speed is
View Solution
