In the List-I below, four different paths of a particle are given as functions of time. In these functions, and are positive constants of appropriate dimensions and . In each case, the force acting on the particle is either zero or conservative. In List-II, five physical quantities of the particle are mentioned: is the linear momentum, is the angular momentum about the origin, is the kinetic energy, is the potential energy and is the total energy. Match each path in List-I with those quantities in List-II, which are conserved for that path.
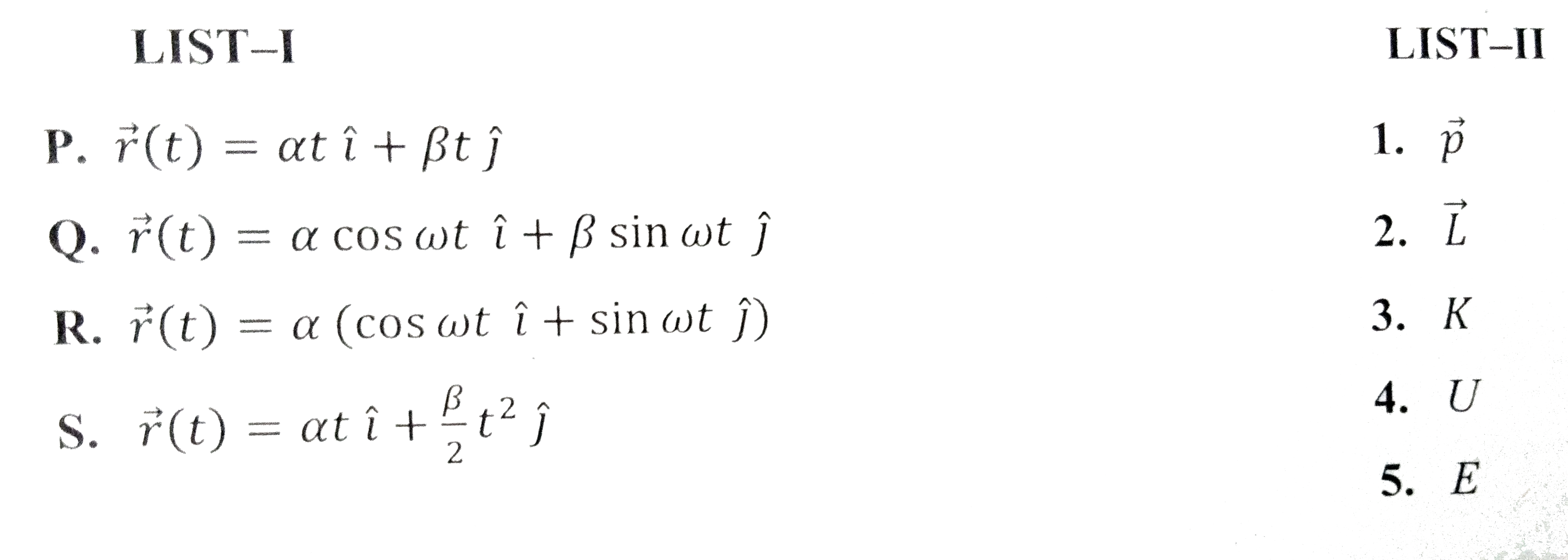
P→1,2,3,4,5,Q→2,5,R→2,3,4,5,S→5
P→1,2,3,4,5,Q→3,5,R→2,3,4,5,S→2,5
P→2,3,4,Q→5,R→1,2,4,S→2,5
P→1,2,3,5,Q→2,5,R→2,3,4,5,S→2.5
The correct Answer is:A
Step by step video, text & image solution for In the List-I below, four different paths of a particle are given as functions of time. In these functions, and are positive constants of appropriate dimensions and . In each case, the force acting on the particle is either zero or conservative. In List-II, five physical quantities of the particle are mentioned: is the linear momentum, is the angular momentum about the origin, is the kinetic energy, is the potential energy and is the total energy. Match each path in List-I with those quantities in List-II, which are conserved for that path. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The angular momentum of a particle is
Aparallel to its linear momentumBperpendicular to its linear momentumCinclined to its linear momentumDa scalar quantity - Question 2 - Select One
The linear momentum p of a particle is given as a function of time t as p=At2+Bt+C.The dimensions of constant B are
A[ML−1T−1]B[ML−1T−2]C[MLT−2]D[MLT−1] - Question 3 - Select One
A particle has a linear momentum p and position vector r. the angular momentum of this particle about the origin will not be zero under the conditions
Ap=0Bp is perpendicular to r and does not cross rCp is anti-parallel to rDthe particle passes through the origin.
The z component of the angular momentum of a particle whose position vector is
View Solutionin a circular motion the angle between a particle's linear momentum and its angular moment is
View SolutionA particle moves on a straight line with a uniform velocity. The angular momentum of the particles is
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
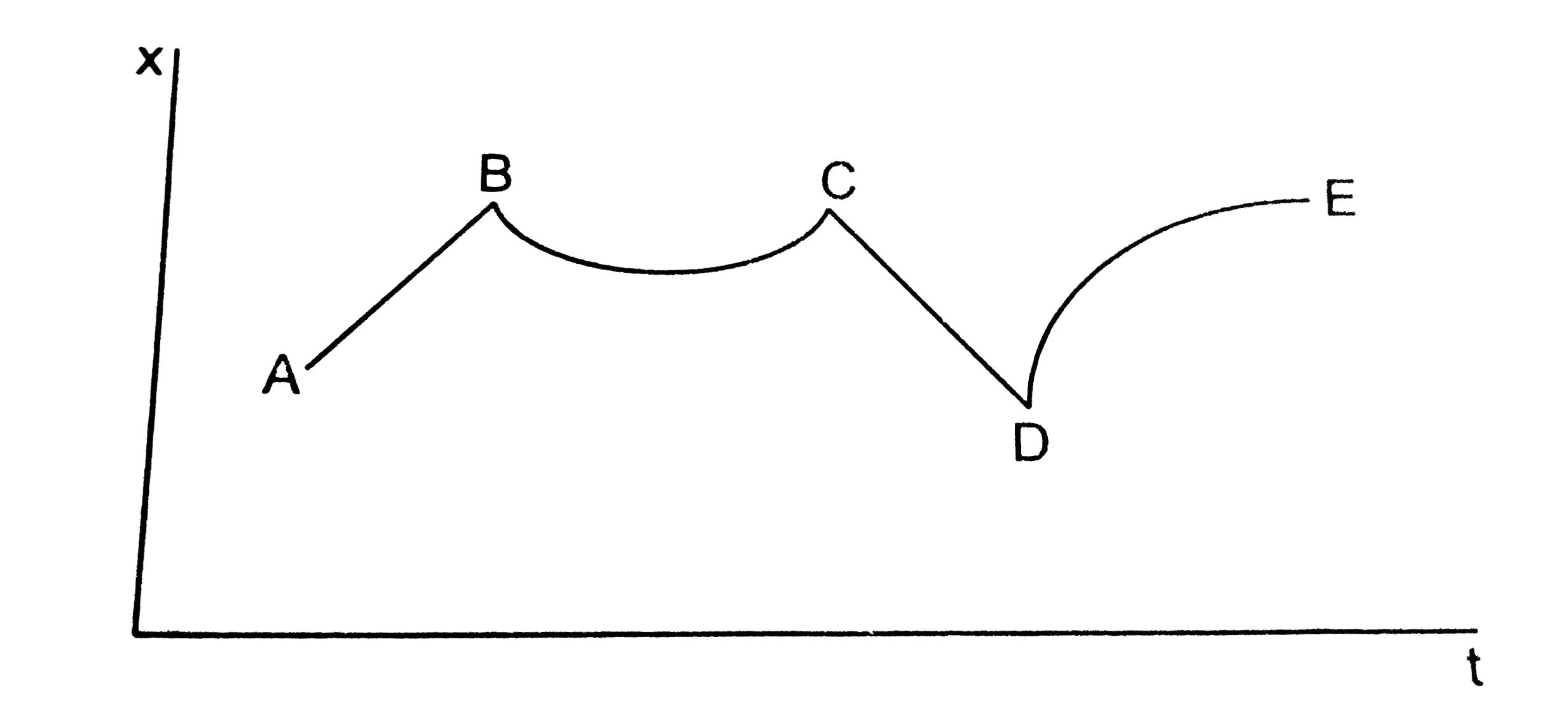 View Solution
View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Its angular momentum about the origin
View Solution

