A positive charge q is placed in a spherical cavity made in a positively charged sphere. The centres of sphere and cavity are displaced by a small distance →l. Force on charge q is :
in the direction parallel to vector →l
in radial direction
in a direction which depends on the magnitude of charge density in sphere
direction can not be determined
The correct Answer is:A
To solve the problem, we need to analyze the situation where a positive charge q is placed in a spherical cavity within a positively charged sphere. The centers of the sphere and the cavity are displaced by a small distance →l. We need to determine the direction of the force acting on the charge q.
1. Understanding the Setup:
- We have a positively charged sphere with a spherical cavity.
- A positive charge q is placed inside this cavity.
- The centers of the sphere and the cavity are displaced by a small distance →l.
2. Electric Field Inside the Sphere:
- The electric field inside a uniformly charged sphere (with charge density ρ) at a distance r from the center is given by:
Esphere=ρr3ϵ0
- Here, ϵ0 is the permittivity of free space.
3. Electric Field Inside the Cavity:
- The electric field inside the cavity (which is empty) can be considered as zero since there are no charges present inside the cavity.
4. Resultant Electric Field:
- The resultant electric field E at the position of charge q is the superposition of the electric field due to the sphere and the cavity:
Eresultant=Esphere−Ecavity=Esphere−0=Esphere
- Therefore, the electric field at the position of charge q is:
E=ρr3ϵ0
5. Displacement Effect:
- Since the centers of the sphere and the cavity are displaced by a distance →l, the position of charge q will also be affected by this displacement.
- The electric field E will depend on the distance l because the effective distance from the center of the sphere to the charge q changes.
6. Direction of the Force:
- The force F on the charge q due to the electric field E is given by:
F=qE
- Since the electric field E is directed radially outward from the center of the positively charged sphere, and considering the displacement →l, the force on charge q will be in the direction parallel to the displacement →l.
7. Conclusion:
- The force on the charge q is in the direction parallel to the vector →l.
Final Answer:
The correct option is: The force on charge q is in the direction parallel to the vector →l.
- We have a positively charged sphere with a spherical cavity.
- A positive charge q is placed inside this cavity.
- The centers of the sphere and the cavity are displaced by a small distance →l.
- The electric field inside a uniformly charged sphere (with charge density ρ) at a distance r from the center is given by:
Esphere=ρr3ϵ0
- Here, ϵ0 is the permittivity of free space.
- The electric field inside the cavity (which is empty) can be considered as zero since there are no charges present inside the cavity.
- The resultant electric field E at the position of charge q is the superposition of the electric field due to the sphere and the cavity:
Eresultant=Esphere−Ecavity=Esphere−0=Esphere
- Therefore, the electric field at the position of charge q is:
E=ρr3ϵ0
- Since the centers of the sphere and the cavity are displaced by a distance →l, the position of charge q will also be affected by this displacement.
- The electric field E will depend on the distance l because the effective distance from the center of the sphere to the charge q changes.
- The force F on the charge q due to the electric field E is given by:
F=qE
- Since the electric field E is directed radially outward from the center of the positively charged sphere, and considering the displacement →l, the force on charge q will be in the direction parallel to the displacement →l.
- The force on the charge q is in the direction parallel to the vector →l.
The correct option is: The force on charge q is in the direction parallel to the vector →l.
Topper's Solved these Questions
- ELECTROSTATICS-IIBOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise 1 (Section D - Plates)
2 Videos
- ELECTROSTATICS-IIBOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise - 2 (Level - I) Section A - Questions Based on electric flux for various configuration, Question on solid angle concept, Gauss law Based Questions
12 Videos
- ELECTROSTATICS-IIBOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise 1 (Section B - Properties of conductors)
15 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
- ERRORS , THEORY BOOK - MOTIONCHAPTER - ERRORS , THEORY EXERCISE - EXERCISE 4 (LEVEL -II)
10 Videos
Similar Questions
A spherical metallic conductor has a spherical cavity. A positive charge is placed inside the cavity at its centre. Another positive charge is placed
View SolutionAsseration: A point charge q is placed at centre of spherical cavity inside a spherical conductor as shown. Another point charge Q is placed outside the conductor as shown. Now as the point charge Q is pushed away from conductor, the potential difference (VA−VB) between two points A and B within the cavity of sphere remains constant.

Reason: The electric field due to charges on outer surface of conductor and outside the conductor is zero at all points inside teh conductor.
View Solution
Knowledge Check
A positive charge q is placed in a spherical cavity made in a positively charged sphere. The centres of sphere and cavity are displaced by a small distance →l. Force on charge q is :
Ain the direction parallel to vectro →lBin radial directionCin a direction which depends on the magitued of charge density in sphereDdirection can not be delermined .A cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is ρ. An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and center of cavity are separated by a distance a. The time after which the electron again touches the sphere is
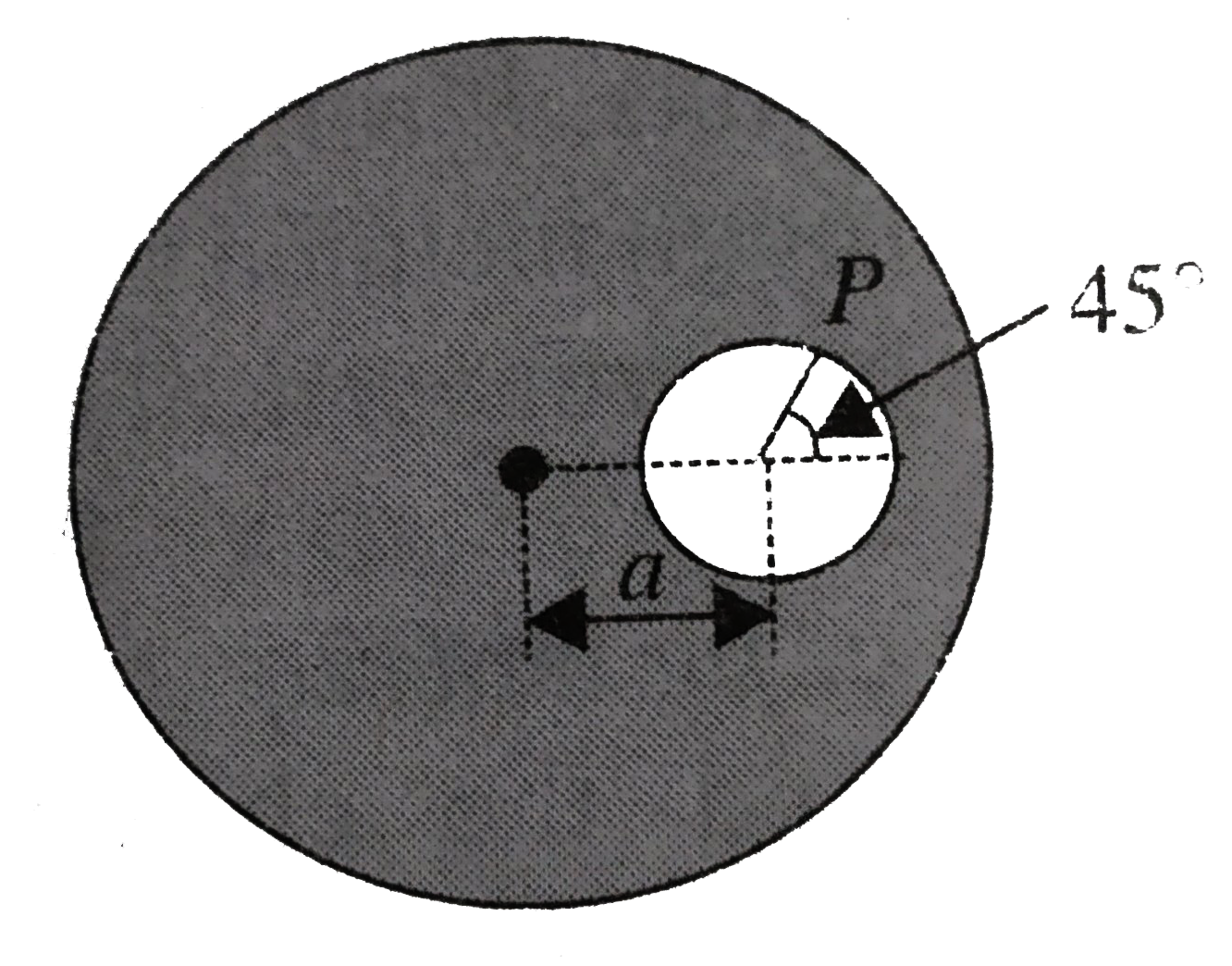 A√6√2rε0mepaB√√2rε0mepaC√6rε0mepaD√rε0mepa
A√6√2rε0mepaB√√2rε0mepaC√6rε0mepaD√rε0mepaA cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is ρ. An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and center of cavity are separated by a distance a. The time after which the electron again touches the sphere is
 A√6√2rε0mepaB√√2rε0mepaC√6rε0mepaD√rε0mepa
A√6√2rε0mepaB√√2rε0mepaC√6rε0mepaD√rε0mepa
A positive point charge q is brought near a neutral metal sphere.
View SolutionThere is a cubical cavity inside a conducting sphere of radius R. A positive point charge Q is placed at the centre of the cube and another positive charge q is placed at a distance 1(>R) from the centre of the sphere. The sphere is earthed
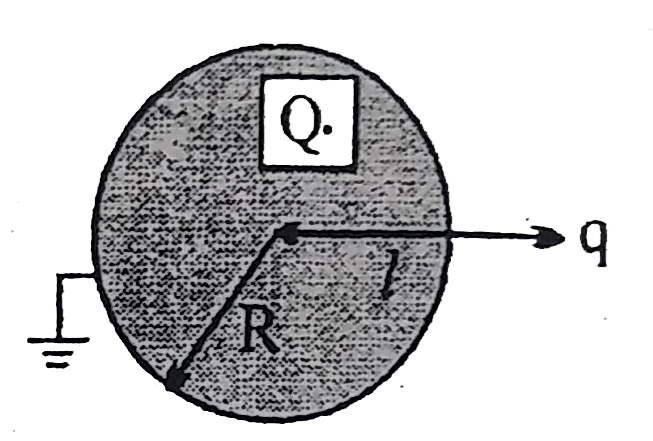
Net charge on the outer surface of conducting sphere is
View SolutionA conducting sphere of radius b has a spherical cavity with its centre displaced by 'a' from centre of sphere O1. A point charged q is placed at the centre of cavity O2. Q charge is given to conducting sphere and charge q0 is placed at P, a distance c from centre O1. Further O1,O2 and P are collinear

View SolutionConsider a conductor with a spherical cavity in it. A point charge q0 is placed at the centre of cavity and a point charge Q is placed outside conductor.
Statement-1: Total charge induced on cavity wall is equal and opposite to the charge inside
Statement-2: If cavity is surrounded by a Gaussian surface, where all parts of Gaussian surface are located inside the conductor, ∮→Ed→A=0 hence q∈duceed=−q0
View SolutionA point charge q1 is placed inside cavity 1 and another point charge q2 is inside cavity 2. A point charge q is placed outside the conductor. For the situation described above, answer the following questions.
If charge q2 is at point Q (inside cavity 2), then →E at the center of cavity 2 due to induced charge on the surface of cavity 2 would be
View Solution
