At t =0Sw is closed , if initially C1 is uncharged and C2 is charged to a potential difference 2∈ then find out following (Given C1=C2=C)
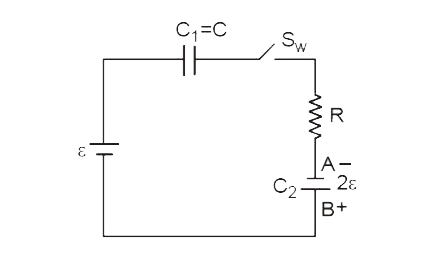
(a) Charge on C1andC2 as a function of time
(b) Find out current in the circuit as a function of time
(c) Also plot the graphs for the relations derived in part (a)
Let q charge flow in time 't' from the battery as shown.The charge on various plates of the capacitor is as shown in the figure
Now applying KVL
∈−qc−iRq−2∈CC=0
∈−qc−qc+2∈−iR=0
3∈=2qC+iR
(##MOTCONJ∃PHYC25SLV042_S01.png width=80%><br> 3in -iR=(2q)/(C) <br> (dq)/( dt) RC=3in C - 2q<br> int _0^(q) (dq)/( 2in C -2q) =int _0^(t) (dt)/( RC) <br> - (1)/(2) ln ((3Cin -2q)/( 3Cin )) =(t)/(RC) <br> 1n ((3in C- 2q)/( 3in C) ) =-( 2t)/(RC) <br> 3in C - 2q=3in C e^(=2 tau//RC) <br> 3in C( 1-e^(-2tau//RC)) = 2q<br> q= (3)/(2) in C(1-e^(-2tau//RC))<br>i =(dq)/( dt) =(3in )/(R) e^(-2t//RC)<br> i =(dq)/( dt) =(3in)/(R) e ^(-2tau//RC)<br>ontheplateB<br> q'=2in C -q<br> 2in C -(3)/(2) in C +(3)/(2) in C e^(-2tau//RC) <br> (##MOT_CON_JEE_PHY_C25_SLV_042_S02.png" width="80%">
=∈C2+32∈Ce−2t/RC=∈C2[1+3e−2τ/RC]
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -160videos
Capacitance
- BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -236videos
Capacitance
- BOOK - MOTIONCHAPTER - CALORIMETRY EXERCISE - EXERCISE - 3 Section - B4videos
CALORIMETRY
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II20videos
CENTRE OF MASS
Similar Questions
At t =0 Sw is closed, if initially C1 is uncharged and C2 is charged to a potential difference 2ε then find out following (Given C1=C2=C)
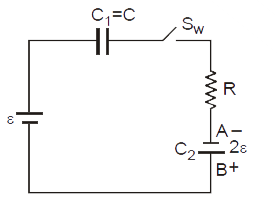
(a) Charge on C1andC2 as a function of time.
(b) Find out current in the circuit as a function of time.
(c) Also plot the graphs for the relations derived in part (a)View SolutionAt t=0, switch is closed, if initially C1 is uncharged and C2 is charged to a potential difference 2ε then find out following (Given C1=C2=C)
(a) Charge on C1 and C2 as a function of time.
(b) Find out current in the circuit as a function of time.
(c) Also plot the graphs for the relations derived in part (a).
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the circuit shown in figure C1=2C2. Capacitance C1 is charged to a potential of V. The current in the circuit just after the switch S is closed is
 AzeroB2VRCinfiniteDV2R
AzeroB2VRCinfiniteDV2R - Question 2 - Select One
In the circuit shown in fig. C1=2C2 Initially, capacitor C1 is charged to a potential of V. The current in the circuit just after the switch S is closed is
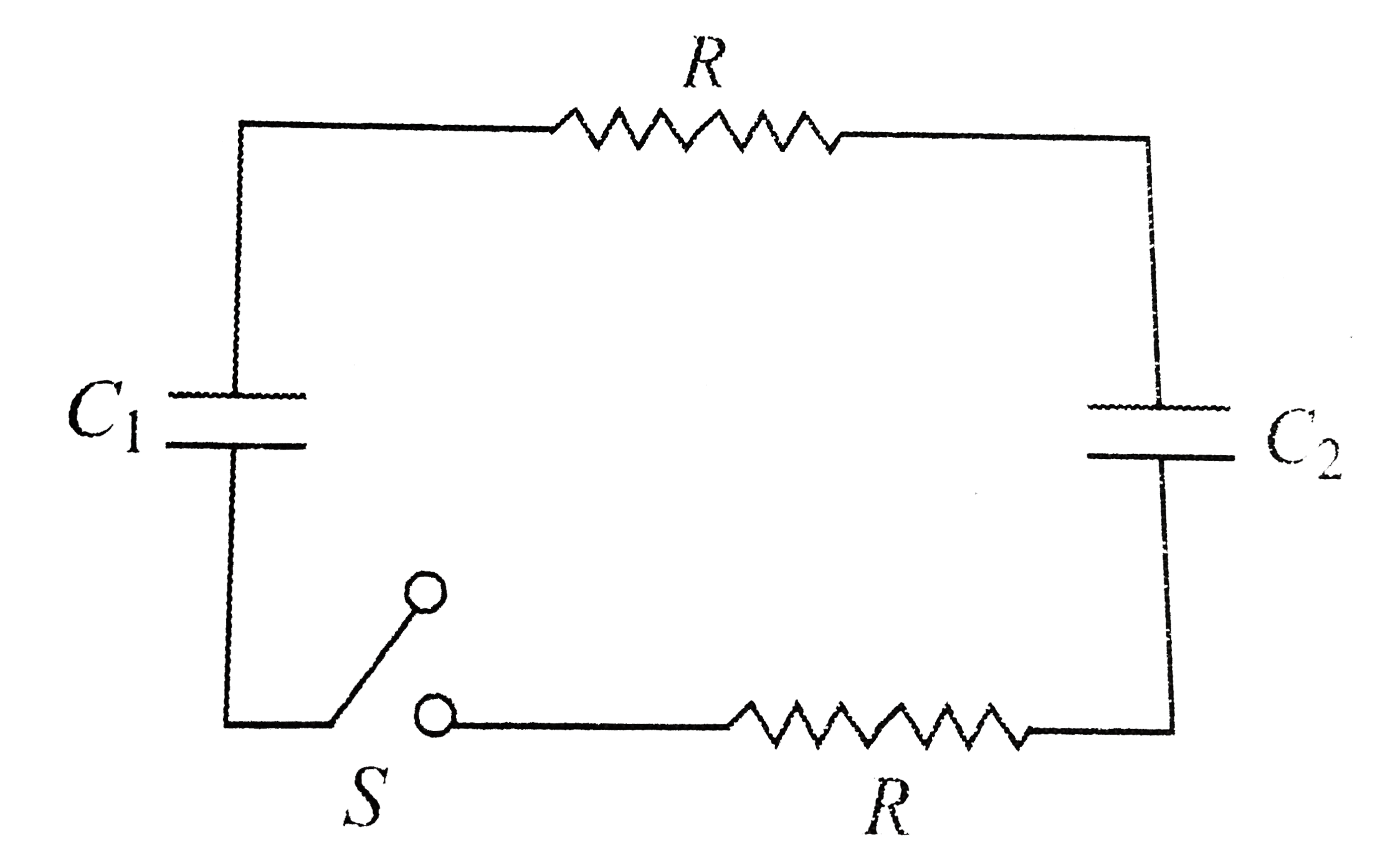 A0B2V/RC∞DV/2R
A0B2V/RC∞DV/2R - Question 3 - Select One or More
A capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
AThe initial current through the resistance is VRBThe current through the resistance as a function of time is i(t)=VRe−tτ where τ=R(C1C2C1+C2)CThe charge on capacitor C1 as a function of time is q1(t)=(C1VC1+C2)(C1+C2e−tτ)DAfter a long time, the potential difference across the capacitor C1is(C1C1+C2)V
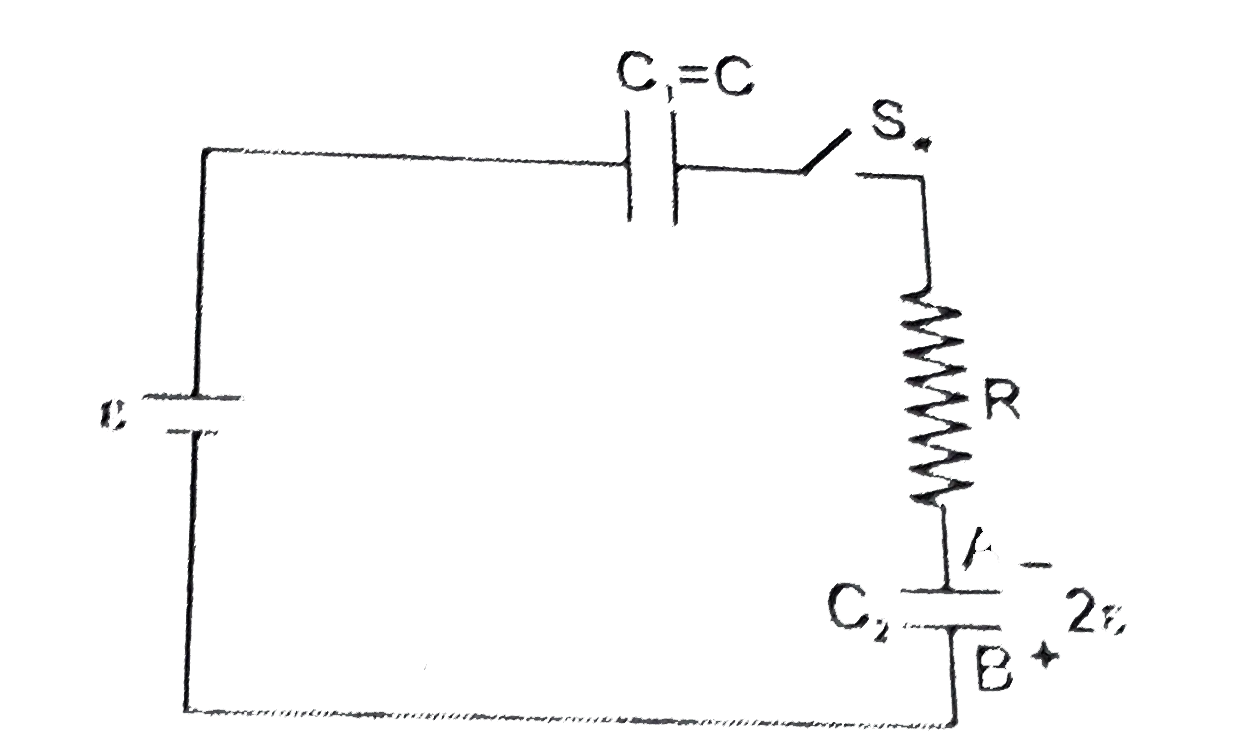
At t=0, switch is closed, if initially C1 is uncharged and C2 is charged to a potential difference 2ε then find out following (Given C1=C2=C)
(a) Charge on C1 and C2 as a function of time.
(b) Also plot the graphs for the relations derived in part (a).
 View Solution
View SolutionIn the circuit shown in figure C1=2C2. Capacitance C1 is charged to a potential of V. The current in the circuit just after the switch S is closed is
 View Solution
View SolutionTwo parallel plate capacitor of capacitance 2C and C are charged to the potentials 2 V and V respectively and are connected in a circuit along with a resistance R as shown in the diagram. The switch k is closed at t=0. Find the current in the circuit as a function of time and total heat produced in the circuit
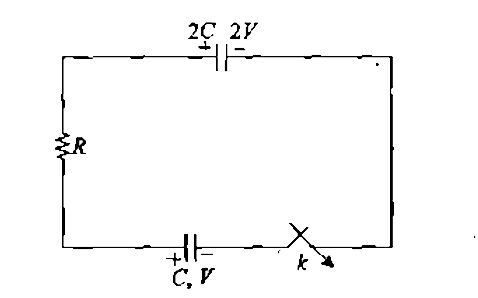 View Solution
View SolutionA capacitor of capacitance C has potential difference E2 and another capacitor of capacitance 2C is uncharged. They are joined to form a closed circuit as shown in the figure.
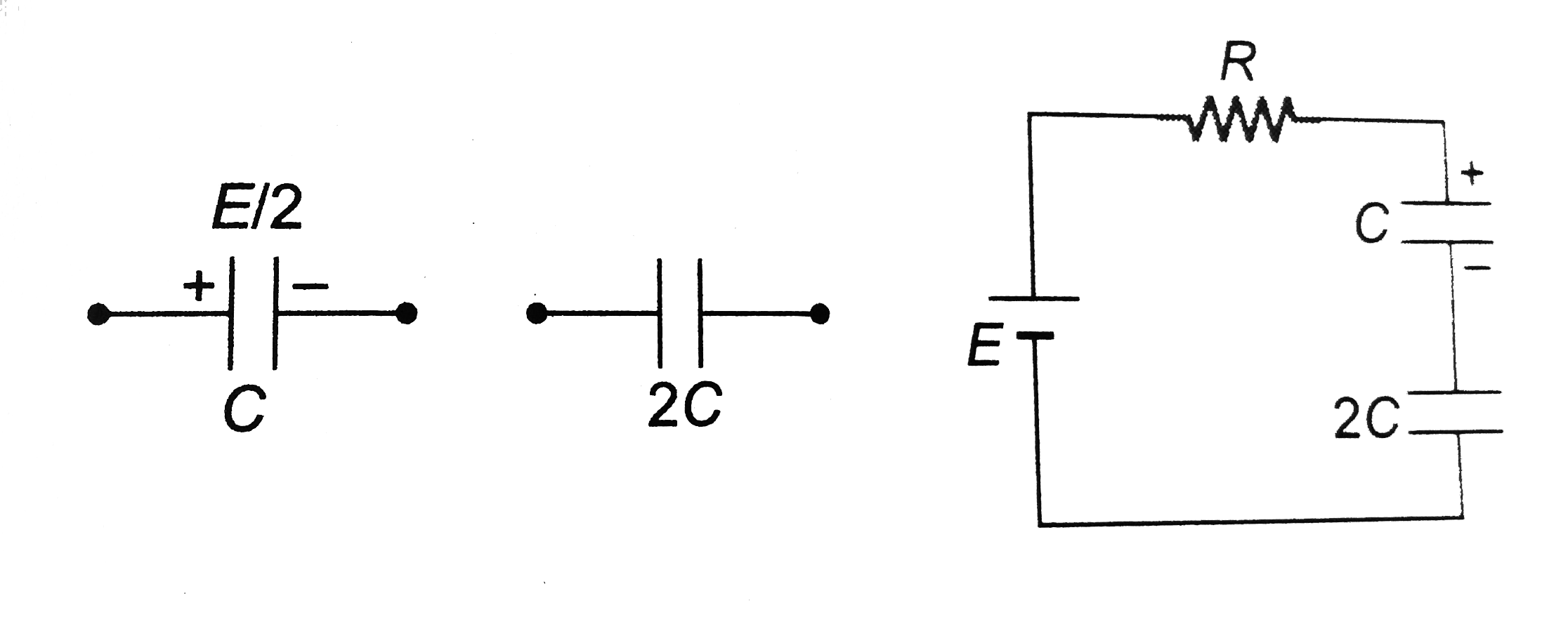
a. Find the current in the circuit at t =0.
b. Find the charge on C as a function of time.View SolutionA capacitor of capacitance C has potential difference E2 and another capacitor of capacitance C is uncharged. They are joined to form a closed circuit as shown in the figure.

a. Find the current in the circuit at t =0.
b. Find the charge on C as a function of time.View Solution
