A parallel plate capacitor of capacitance C has spacing d between two plates having area A. The region between the plates is filled with N dielectric layers, parallel to its plates, each with thickness
δ=dN .The dielectric constant of the mth layer is Km=K(1+mN). For a very large N(<103), the capacitance C is α(k∈0Ad1n2) .The value of αwillbe.<br> [in _0 is the permittivity of free space ]
The correct Answer is:A
Step by step video, text & image solution for A parallel plate capacitor of capacitance C has spacing d between two plates having area A. The region between the plates is filled with N dielectric layers, parallel to its plates, each with thickness delta =(d)/(N) .The dielectric constant of the m^(th) layer is K_m =K(1+(m)/(N)) . For a very large N(lt 10 ^(3)) , the capacitance C is alpha ((kin_0A)/( d1n 2)) .The value of alpha will be . [in _0 is the permittivity of free space ] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A parallel plate capacitor of capacitance has spacing between two plates having area The region between the plates is filled with dielectric layers, parallel to its plates, each with thickness δ=dN. The dielectric constant of the mth layer is Km=K(1+mN). For a very large N(>103), the capacitance Cisα(K∈0Adln2). Find the value of α.[∈0 is the permittivity of free space]
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View Solution
Knowledge Check
- Question 1 - Select One
A parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
A3CBC3C12 CDC6 - Question 2 - Select One
A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.
 A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)
A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1) - Question 3 - Select One
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
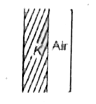 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
A parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View SolutionA parallel plate capacitor is filled with dielectrics. What is capacitance?
 View Solution
View SolutionA parallel plate capacitor with air between the plates has capacitance of 9pF. The separation between its plates is 'd'. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant k1=3 and thickness d3 while the other one has dielectric constant k2=6 and thickness 2d3. Capacitance of the capacitor is now
View SolutionA parallel plate capacitor with air between the plates has a capacitance of 9 pF. The separation between its plates is ‘d'. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant K1=3 and thickness d3 while the other one has dielectric constant K2=6 and thickness 23d. Capacitance of the capacitor is now
View SolutionA parallel plate capacitor with oil as a dielectric between the plates has a capacitance C. if the oil, with dielectric constannt (K=3), is removed, then the capacitance of the capacitor will be
View Solution

