A parallel plate capacitor of capacitance has spacing between two plates having area The region between the plates is filled with dielectric layers, parallel to its plates, each with thickness δ=dN. The dielectric constant of the mth layer is Km=K(1+mN). For a very large N(>103), the capacitance Cisα(K∈0Adln2). Find the value of α.[∈0 is the permittivity of free space]
The correct Answer is:1.00
To solve the problem, we need to find the value of α in the expression for the capacitance of a parallel plate capacitor filled with multiple dielectric layers. Let's break down the solution step by step.
Step 1: Understand the Configuration
We have a parallel plate capacitor with:
- Area A
- Plate separation d
- The space between the plates is filled with N dielectric layers, each of thickness δ=dN.
Step 2: Dielectric Constant of Each Layer
The dielectric constant for the mth layer is given by:
Km=K(1+mN)
where K is a constant.
Step 3: Capacitance of Each Layer
The capacitance Cm of each dielectric layer can be expressed as:
Cm=Kmϵ0Aδ
Substituting δ=dN:
Cm=Kmϵ0ANd
Step 4: Substitute for Km
Substituting Km into the capacitance formula:
Cm=K(1+mN)ϵ0ANd
Step 5: Total Capacitance
Since the capacitors are in series, the total capacitance C can be found using:
1C=N∑m=11Cm
Substituting for Cm:
1C=N∑m=1dK(1+mN)ϵ0AN
Step 6: Simplifying the Summation
Factoring out constants:
1C=dKϵ0ANN∑m=111+mN
Let x=mN, then the summation can be approximated by an integral as N becomes very large:
N∑m=111+mN≈N∫1011+xdx
Calculating the integral:
∫1011+xdx=ln(2)
Step 7: Substitute Back into the Capacitance Formula
Thus, we have:
1C≈dKϵ0A⋅ln(2)
Taking the reciprocal gives:
C≈Kϵ0Adln(2)
Step 8: Identify α
From the problem statement, we have:
C=αKϵ0Adln(2)
Comparing both expressions, we find:
α=1
Final Answer
The value of α is:
α=1
We have a parallel plate capacitor with:
- Area A
- Plate separation d
- The space between the plates is filled with N dielectric layers, each of thickness δ=dN.
The dielectric constant for the mth layer is given by:
Km=K(1+mN)
where K is a constant.
The capacitance Cm of each dielectric layer can be expressed as:
Cm=Kmϵ0Aδ
Substituting δ=dN:
Cm=Kmϵ0ANd
Substituting Km into the capacitance formula:
Cm=K(1+mN)ϵ0ANd
Since the capacitors are in series, the total capacitance C can be found using:
1C=N∑m=11Cm
Substituting for Cm:
1C=N∑m=1dK(1+mN)ϵ0AN
Factoring out constants:
1C=dKϵ0ANN∑m=111+mN
Let x=mN, then the summation can be approximated by an integral as N becomes very large:
N∑m=111+mN≈N∫1011+xdx
Calculating the integral:
∫1011+xdx=ln(2)
Thus, we have:
1C≈dKϵ0A⋅ln(2)
Taking the reciprocal gives:
C≈Kϵ0Adln(2)
From the problem statement, we have:
C=αKϵ0Adln(2)
Comparing both expressions, we find:
α=1
The value of α is:
α=1
Similar Questions
A parallel plate capacitor of capacitance C has spacing d between two plates having area A. The region between the plates is filled with N dielectric layers, parallel to its plates, each with thickness
δ=dN .The dielectric constant of the mth layer is Km=K(1+mN). For a very large N(<103), the capacitance C is α(k∈0Ad1n2) .The value of αwillbe.<br> [in _0 is the permittivity of free space ]View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View Solution
Knowledge Check
- Question 1 - Select One
A parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
A3CBC3C12 CDC6 - Question 2 - Select One
A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.
 A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)
A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1) - Question 3 - Select One
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
Two identical parallel plate (air) capacitors c1andc2 have capacitances C each. The space between their plates is now filled with dielectrics as shown. If two capacitors still have equal capacitance, obtain the relation betweenn dielectric constants k,k1andk2.
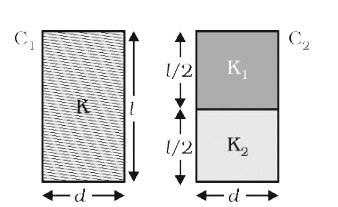 View Solution
View SolutionA parallel plate capacitor with air inbetween the paltes has a capacitance of 8 pF. The separation between the plates is now reduced by half and the space between them is filled with a medium of dielectric constant 5.
Calculate the new value of capacitance.View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View SolutionA parallel plate capacitor with air between the plates has a capacitance of 10 pF. The capacitance, if the distance bgetween the plates is reduced by half and the space between tehm is filled with a substance of dielectric constant 4 is
View SolutionA parallel plate capacitor with air between the plates has capacitance of 9pF. The separation between its plates is 'd'. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant k1=3 and thickness d3 while the other one has dielectric constant k2=6 and thickness 2d3. Capacitance of the capacitor is now
View Solution

