Three identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
1.67×10−11(ˆi+ˆj)N
3.34×10−10(ˆi+ˆj)N
1.67×10−7(ˆi+ˆj)N
3.34×10−10(ˆi+ˆj)N
The correct Answer is:C
Step by step video, text & image solution for Three identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 1 (Section - A :- Newtons Law of Gravitation & Gravitational Field, Potential and Potential Energy)28videos
GRAVITATION
- BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 1 (Section - B :- Gravitational Acceleration and Its Variation)20videos
GRAVITATION
- BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 4 | Level - II (Previous Year | JEE Advanced)15videos
GRAVITATION
- BOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 4 | Level-II55videos
GEOMETRICAL OPTICS
- BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -4 (Level - II) Previous Year | JEE Advanced22videos
HEAT - 1
Similar Questions
Three point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree balls each of mass 0.5 kg are kept at the vertices of an isosceles right triangle with its hypotenuse of 2√2 m. What will be the net gravitational force on the ball kept at the vertex of right angle ?
View Solution
Knowledge Check
- Question 1 - Select One
The centre of mass of three bodies each of mass 1 kg located at the points (0,0), (3, 0) and (0, 4) in the x-y plane is
A(43,1)B(13,23)C(12,12)D(1,43) - Question 2 - Select One
A large number of identical point masses m are placed along x - axis ,at x = 0,1,2,4,……… The magnitude of gravitational force on mass at origin ( x =0) , will be
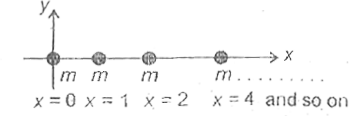 AGm2B43Gm2C23Gm2D54Gm2
AGm2B43Gm2C23Gm2D54Gm2 - Question 3 - Select One
An equation of the plane through the points (1,0,0), (0,2,0) and at a distance 6/7 units from the origin, is
A6x+3y+z−6=0B6x+3y+2z−6=0C6x+3y+z+6=0D6x+3y+2z+6+0
Three point masses of 1kg,2kgand3kg lie at (1,2),(0,−1)and(2,−3) respectively. Calculate the co-ordinates of the centre of mass of the system.
View SolutionTwo bodies of masses 1 kg and 3 kg are lying in xy plane at (0, 0) and (2, -1) respectively. What are the coordinates of the centre of mass ?
View SolutionThree identical particles each of mass 0.1kg are arranged at three corners of a square of side √2m. The distance of the centre of mass from the fourth corners is
View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass isView SolutionFour identical masses m each are kept at points A, B, C & D shown in figure. Gravitational force on mass at point D (body centre) is -
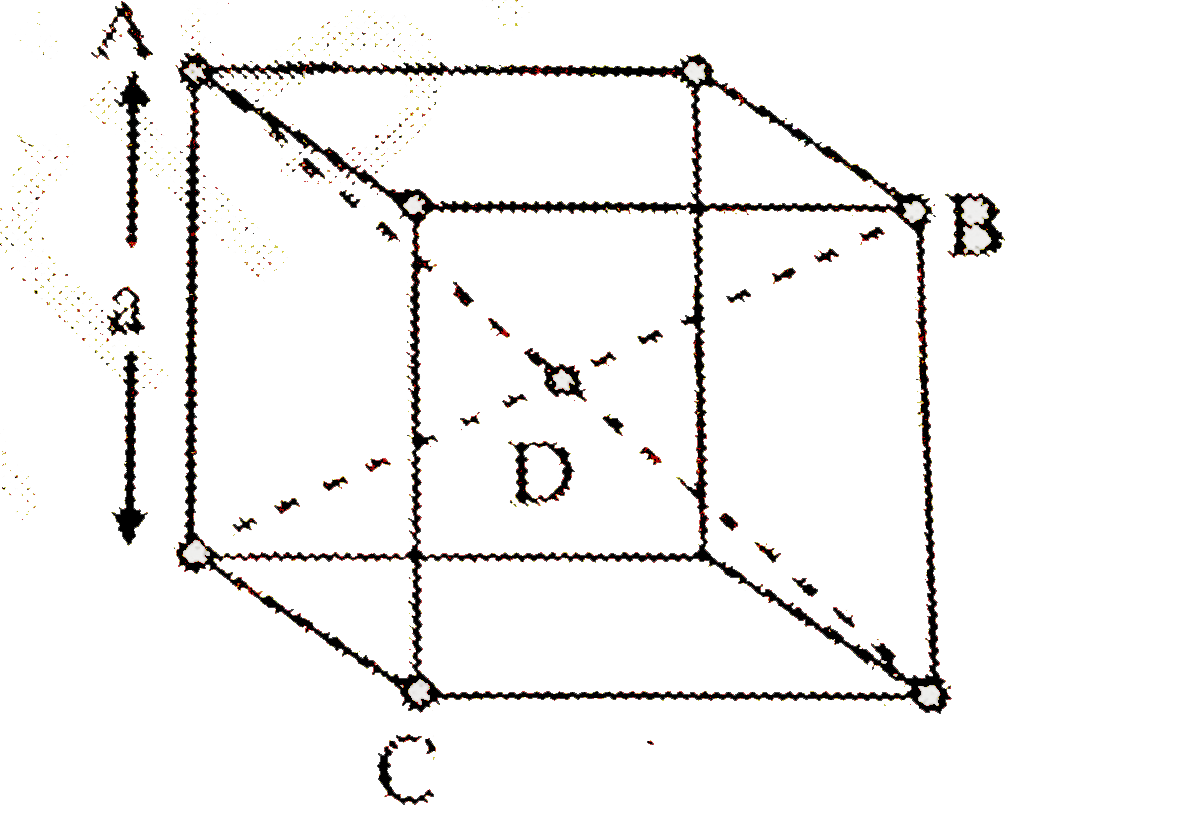 View Solution
View Solution

