A string of length 1 m is fixed at one end and carries a mass of 100 gm at the other end. The string makes (2/π) revolutions per second around vertical axis through the fixed end. Calculate the tension in the string-
1.0 N
1.6 N
2N
4N
The correct Answer is:B
To solve the problem of finding the tension in the string, we can follow these steps:
Step 1: Understand the Given Information
- Length of the string (L) = 1 m
- Mass (m) = 100 gm = 0.1 kg (convert grams to kilograms)
- Revolutions per second (f) = 2π rev/s
Step 2: Convert Revolutions per Second to Radians per Second
To find the angular velocity (ω) in radians per second, we use the conversion:
ω=2πf
Substituting the value of f:
ω=2π(2π)=4 rad/s
Step 3: Identify the Radius of Circular Motion
Since the string is fixed at one end and the mass is at the other end, the radius (r) of the circular motion is equal to the length of the string:
r=L=1 m
Step 4: Calculate the Centripetal Force
The tension in the string provides the necessary centripetal force for the circular motion. The formula for centripetal force (F_c) is:
Fc=mv2r
where v is the linear velocity. We can express v in terms of ω and r:
v=rω
Substituting r=1 m and ω=4 rad/s:
v=1×4=4 m/s
Step 5: Substitute Values into the Centripetal Force Formula
Now we can substitute v back into the centripetal force formula:
Fc=m(v2)r=0.1×(42)1
Calculating v2:
v2=16 m2/s2
Now substituting:
Fc=0.1×161=1.6 N
Step 6: Conclusion
The tension in the string, which is equal to the centripetal force required for the circular motion, is:
T=1.6 N
Final Answer
The tension in the string is 1.6 N.
---
- Length of the string (L) = 1 m
- Mass (m) = 100 gm = 0.1 kg (convert grams to kilograms)
- Revolutions per second (f) = 2π rev/s
To find the angular velocity (ω) in radians per second, we use the conversion:
ω=2πf
Substituting the value of f:
ω=2π(2π)=4 rad/s
Since the string is fixed at one end and the mass is at the other end, the radius (r) of the circular motion is equal to the length of the string:
r=L=1 m
The tension in the string provides the necessary centripetal force for the circular motion. The formula for centripetal force (F_c) is:
Fc=mv2r
where v is the linear velocity. We can express v in terms of ω and r:
v=rω
Substituting r=1 m and ω=4 rad/s:
v=1×4=4 m/s
Now we can substitute v back into the centripetal force formula:
Fc=m(v2)r=0.1×(42)1
Calculating v2:
v2=16 m2/s2
Now substituting:
Fc=0.1×161=1.6 N
The tension in the string, which is equal to the centripetal force required for the circular motion, is:
T=1.6 N
The tension in the string is 1.6 N.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 2
16 Videos
- CIRCULAR MOTIONBOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 3 SECTION -A
14 Videos
- CIRCULAR MOTIONBOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 4
16 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II
20 Videos
- COMMUNICATION SYSTEMBOOK - MOTIONCHAPTER - COMMUNICATION SYSTEMEXERCISE - EXERCISE - 3
6 Videos
Similar Questions
A string of length 50cm is fixed at one end and carries a mass of 200g at the other end. The string makes 5/2π revolution per second around the verticle axis through the fixed end. Calculate (a) the tension in the string (b) the angle of incilination of the string with verticle and (c) linear velocity of the mass.
View SolutionA string of length 1 m is fixed at one end and carries a mass of 100 gm at the other end. The string makes 2/πrevolutions per second about a vertical axis through the fixed end. The angle of inclination of the string with the vertical, and the linear velocity of the mass will respec- tively be - (in M.K.S. system)
View Solution
Knowledge Check
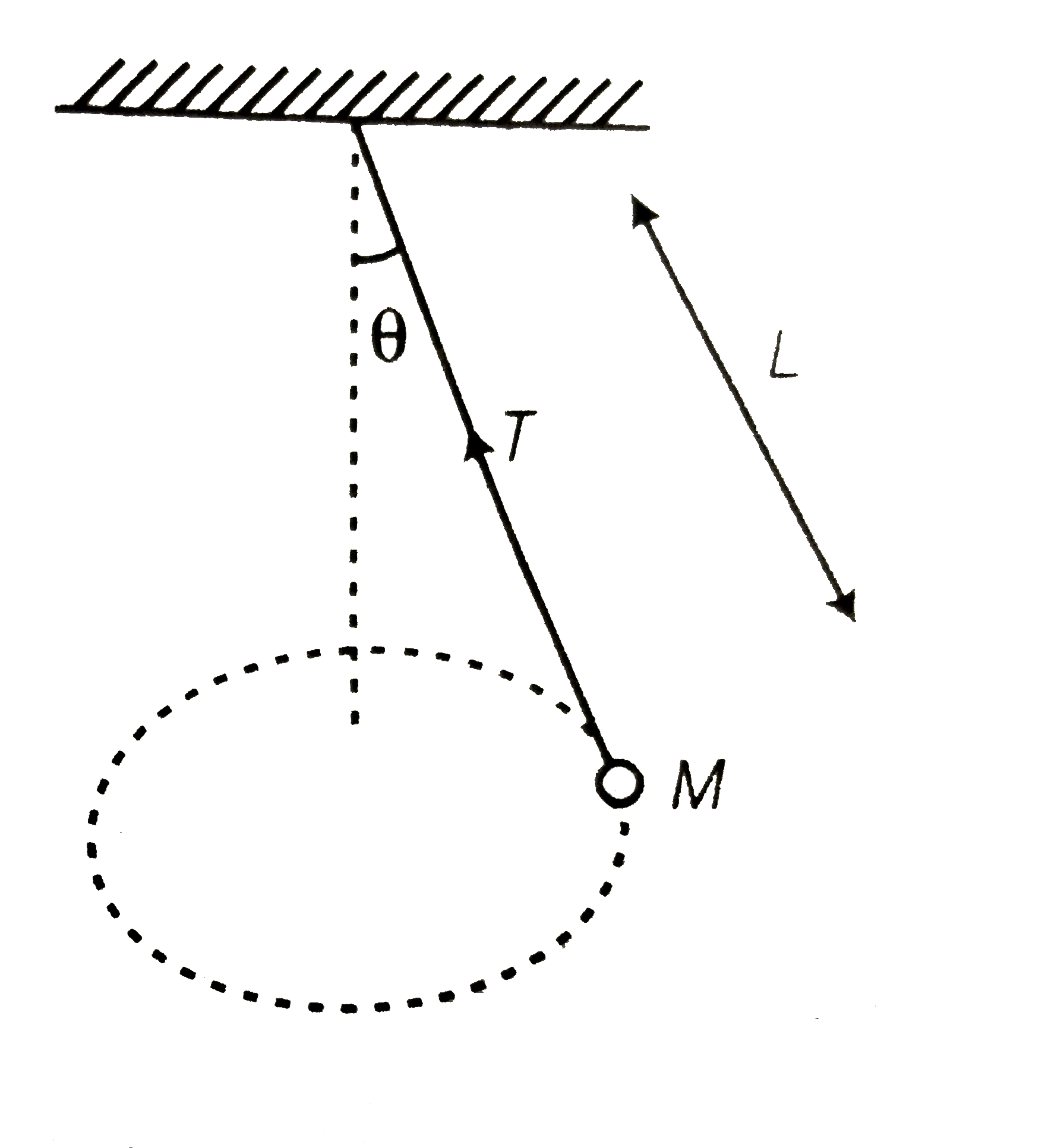
A string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/π revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.
 AMLB2MLC4MLD16ML
AMLB2MLC4MLD16MLA string of length l=1m is fixed at one end carries a mass of 100gm at other end. The string makes √5/(π) revolutions per second about a verticle axis passing through its second end. What is the angle of inclination of the string with the vertical?
A30∘B45∘C60∘D75∘A string of length l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
 A16 mlB4 mlC8 mlD2 ml
A16 mlB4 mlC8 mlD2 ml
A string of length 1m is fixed at one end and carries a mass of 1 kg at the other end. The string makes 2/π revolutions per second around a vertical axis passing through the fixed end. Calculate (i) angle of inclination of the string with the vertical, (ii) the tension in the strong and (iii) the linear velocity of the mass.
View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes 2π rev/s around the vertical axis through the fixed end as shown in figure, then tension in string is
View SolutionVibrations of string fixed at one end
View SolutionIn a conical pendulum arrangement, a string of length 1 m is fixed at one end with a bob of mass 100g and the string makes 4radpersec around a vertical axis through a fixed point. The angle of inclination of the string with vertical is: (Take g=10ms−1)
View SolutionIn a conical pendulum arrangement, a string of length 1 m is fixed at one end with a bob of mass 100 g and the string makes 2πmvs−1around a vertical axis through a fixed point. The angle of inclination of the string with vertical is: (Take g=10ms−1)
View Solution
