In a conical pendulum arrangement, a string of length 1 m is fixed at one end with a bob of mass 100 g and the string makes 2πmvs−1around a vertical axis through a fixed point. The angle of inclination of the string with vertical is: (Take g=10ms−1)
tan−1(58)
tan−1(35)
cos−1(85)
cos−1(58)
The correct Answer is:D
To solve the problem of finding the angle of inclination of the string with the vertical in a conical pendulum arrangement, we can follow these steps:
Step 1: Understand the Forces Acting on the Bob
In a conical pendulum, the forces acting on the bob are:
- The tension T in the string, which has two components:
- Tcosθ acting vertically upwards (balancing the weight)
- Tsinθ acting horizontally (providing the centripetal force)
- The weight of the bob mg acting downwards.
Step 2: Set Up the Equations
From the balance of forces, we can write the following equations:
1. Vertical Force Balance:
Tcosθ=mg
2. Horizontal Force (Centripetal Force):
Tsinθ=mv2r
where r is the horizontal radius of the circular path traced by the bob.
Step 3: Express r in Terms of θ
The radius r can be expressed in terms of the length of the string L and the angle θ:
r=Lsinθ
Step 4: Substitute r into the Centripetal Force Equation
Substituting r into the horizontal force equation gives:
Tsinθ=mv2Lsinθ
Step 5: Divide the Two Equations
Dividing the horizontal force equation by the vertical force equation:
TsinθTcosθ=mv2Lsinθmg
This simplifies to:
tanθ=v2gL
Step 6: Substitute the Given Values
We know:
- L=1m
- m=0.1kg (100 g)
- g=10ms−2
- The speed v=2πm/s
Substituting v:
tanθ=(2π)210×1
Calculating v2:
v2=(2π)2=4π2
Thus,
tanθ=4π210=410π2=25π2
Step 7: Find θ
To find θ, we take the arctangent:
θ=tan−1(25π2)
Step 8: Calculate the Angle
Using a calculator, we can find the approximate value of θ.
Final Result
The angle of inclination θ can be approximated numerically.
In a conical pendulum, the forces acting on the bob are:
- The tension T in the string, which has two components:
- Tcosθ acting vertically upwards (balancing the weight)
- Tsinθ acting horizontally (providing the centripetal force)
- The weight of the bob mg acting downwards.
From the balance of forces, we can write the following equations:
1. Vertical Force Balance:
Tcosθ=mg
2. Horizontal Force (Centripetal Force):
Tsinθ=mv2r
where r is the horizontal radius of the circular path traced by the bob.
The radius r can be expressed in terms of the length of the string L and the angle θ:
r=Lsinθ
Substituting r into the horizontal force equation gives:
Tsinθ=mv2Lsinθ
Dividing the horizontal force equation by the vertical force equation:
TsinθTcosθ=mv2Lsinθmg
This simplifies to:
tanθ=v2gL
We know:
- L=1m
- m=0.1kg (100 g)
- g=10ms−2
- The speed v=2πm/s
tanθ=(2π)210×1
Calculating v2:
v2=(2π)2=4π2
Thus,
tanθ=4π210=410π2=25π2
To find θ, we take the arctangent:
θ=tan−1(25π2)
Using a calculator, we can find the approximate value of θ.
The angle of inclination θ can be approximated numerically.
Similar Questions
A string of length 1 m is fixed at one end and carries a mass of 100 gm at the other end. The string makes 2/πrevolutions per second about a vertical axis through the fixed end. The angle of inclination of the string with the vertical, and the linear velocity of the mass will respec- tively be - (in M.K.S. system)
View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes 2π rev/s around the vertical axis through the fixed end as shown in figure, then tension in string is
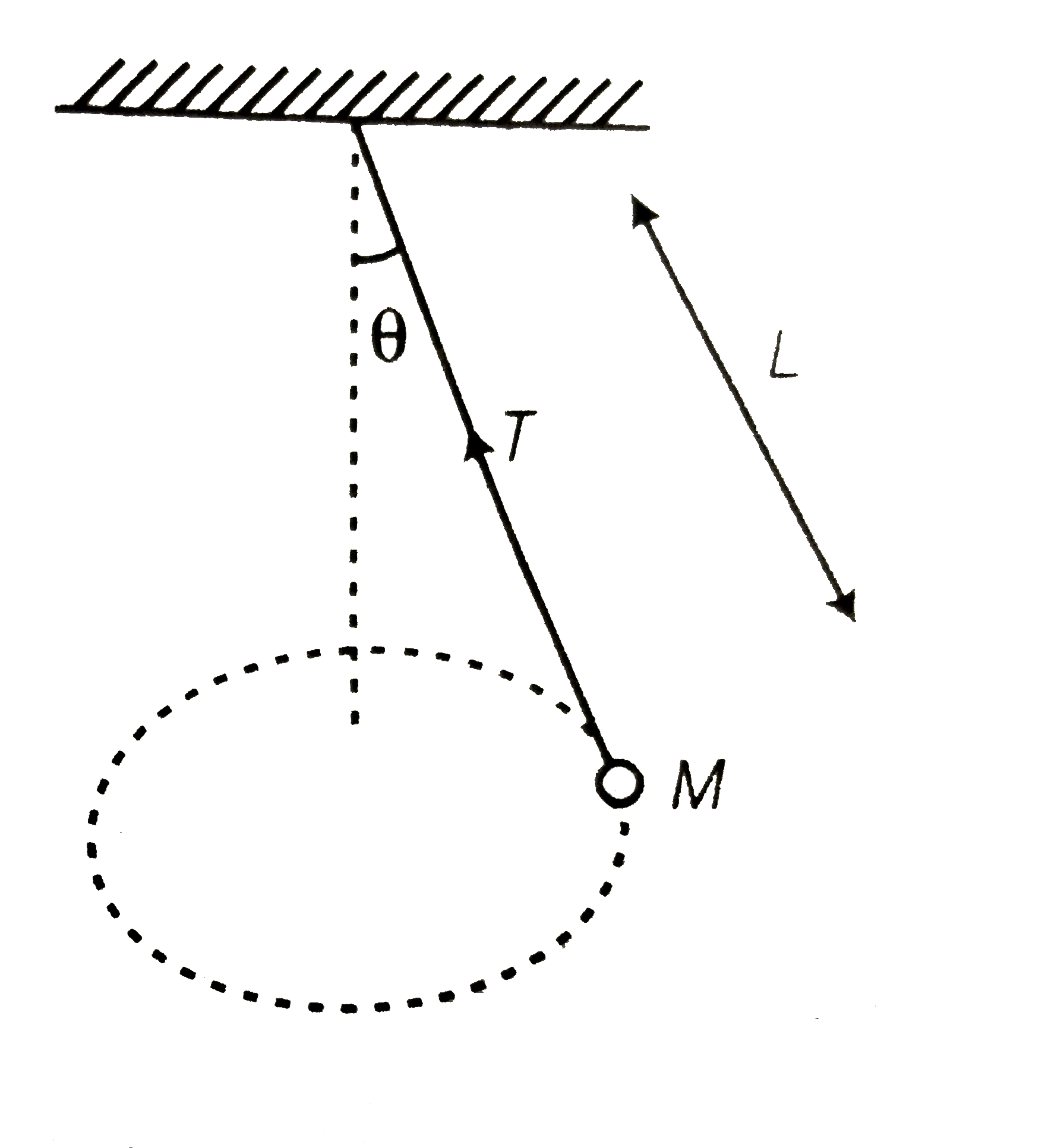
View Solution
Knowledge Check
In a conical pendulum arrangement, a string of length 1 m is fixed at one end with a bob of mass 100g and the string makes 4radpersec around a vertical axis through a fixed point. The angle of inclination of the string with vertical is: (Take g=10ms−1)
Atan−1(58)Btan−1(35)Ccos−1(35)Dcos−1(58)A string of length l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
 A16 mlB4 mlC8 mlD2 ml
A16 mlB4 mlC8 mlD2 mlA string of length l=1m is fixed at one end carries a mass of 100gm at other end. The string makes √5/(π) revolutions per second about a verticle axis passing through its second end. What is the angle of inclination of the string with the vertical?
A30∘B45∘C60∘D75∘
A string of length 1m is fixed at one end and carries a mass of 1 kg at the other end. The string makes 2/π revolutions per second around a vertical axis passing through the fixed end. Calculate (i) angle of inclination of the string with the vertical, (ii) the tension in the strong and (iii) the linear velocity of the mass.
View SolutionA string of length 50cm is fixed at one end and carries a mass of 200g at the other end. The string makes 5/2π revolution per second around the verticle axis through the fixed end. Calculate (a) the tension in the string (b) the angle of incilination of the string with verticle and (c) linear velocity of the mass.
View SolutionA string of length 0.5 m carries a bob of mass 0.1 kg at its end. If this is to be used as a concial pendulum of period 0.4πs s, calculate the angle of inclination of the string with the vertical and the tension in the string .
View SolutionA string of length 1 m is fixed at one end and carries a mass of 100 gm at the other end. The string makes (2/π) revolutions per second around vertical axis through the fixed end. Calculate the tension in the string-
View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/π revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.

View Solution
