On suspending a mass m from a spring of force constant k, frequency of vibration f is obtained. If a second spring as shown in the figure, is arranged then the frequency will be :

f√2
f/√2
2f
f
The correct Answer is:A
Step by step video & image solution for On suspending a mass m from a spring of force constant k, frequency of vibration f is obtained. If a second spring as shown in the figure, is arranged then the frequency will be : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - A Previous Year Problems | NEET
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
23 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -1 (Objective Problems | NEET) SECTION-E Simple Pendulum
6 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -4 (Leve-II) [ JEE 2011]
11 Videos
Similar Questions
Two spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View SolutionA mass m attached to a spring A has a frequency of 3 Hz and a spring B has a frequency of 4 Hz.When both spring are connected as shown in the figure, Find the frequency (in Hz)of oscillation.
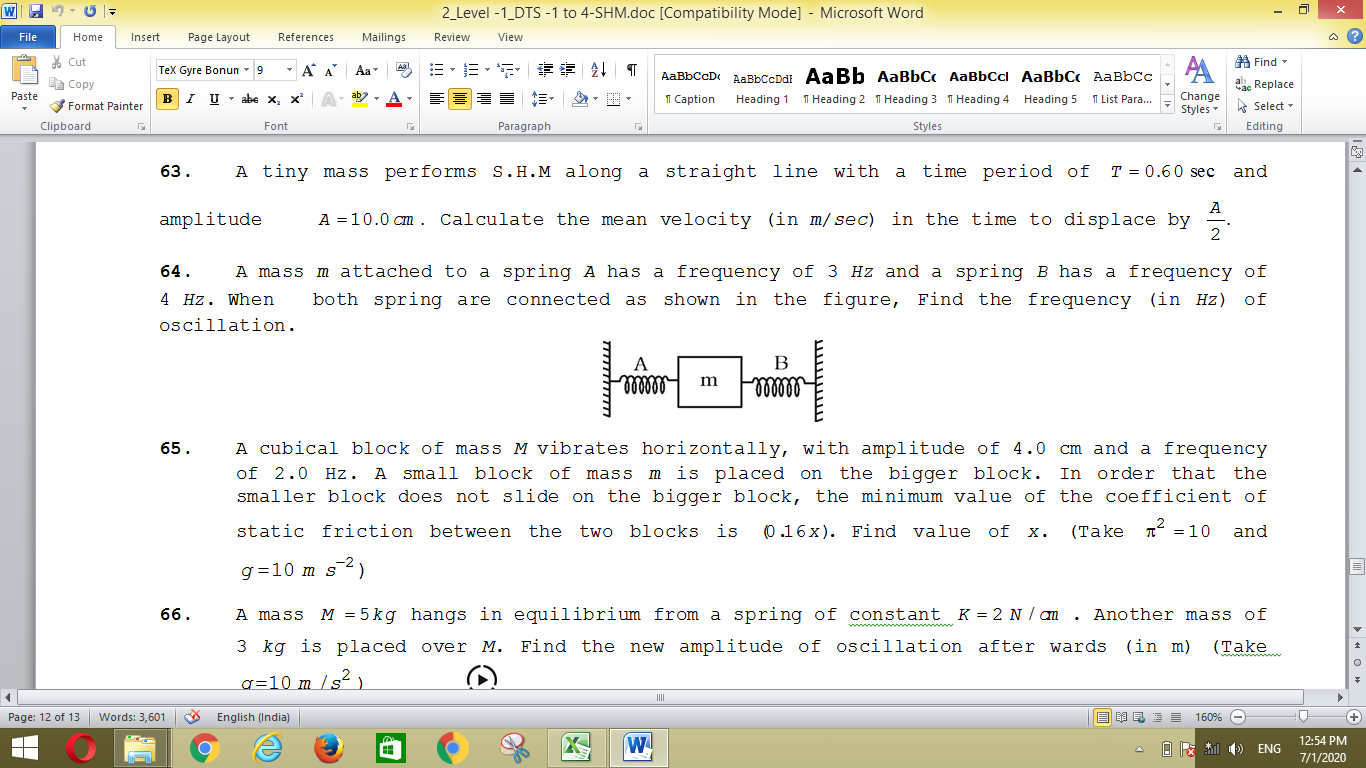
View Solution
Knowledge Check
The frequency of vertical oscillations of the three spring-mass system, shown in figure, is
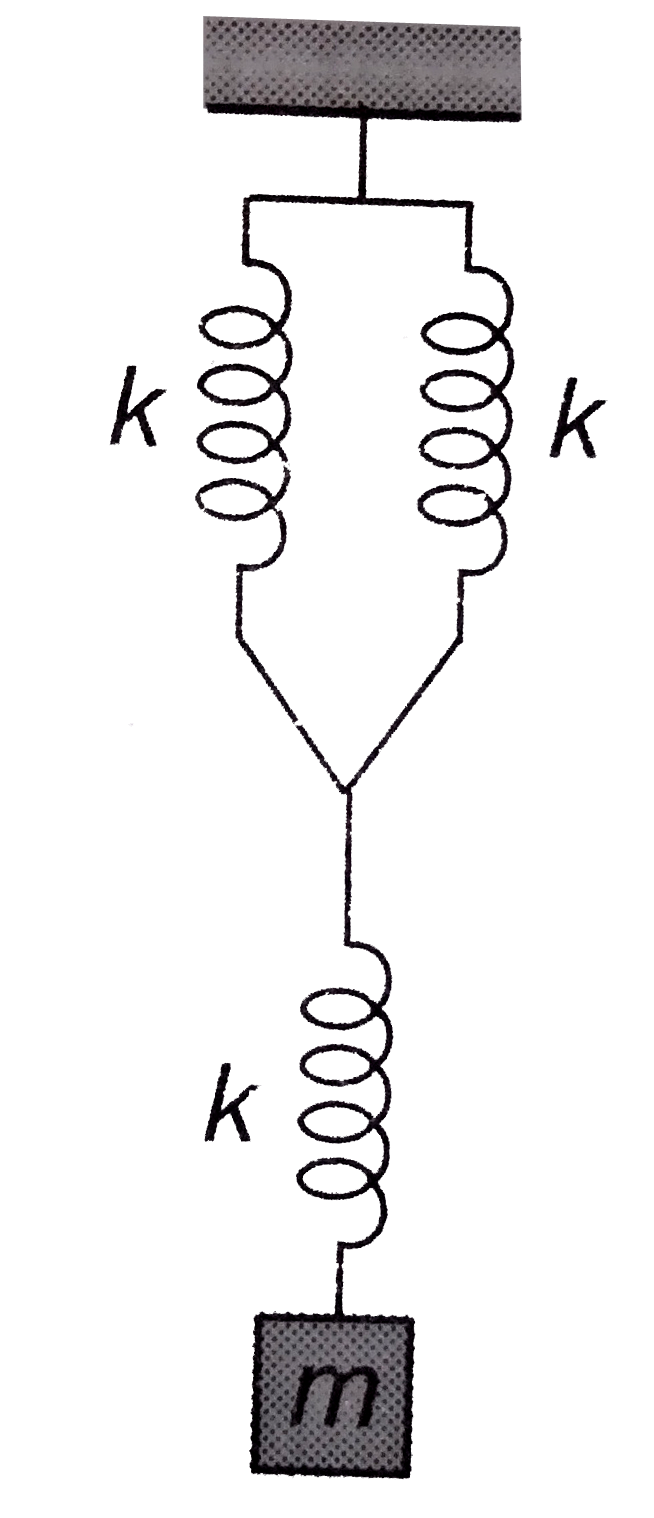 A12π√3k2mB12π√2k3mC12π√2kmD12π√k3m
A12π√3k2mB12π√2k3mC12π√2kmD12π√k3mThe frequency of oscillation of the springs shown in the figure will be
 A12π√KmB12π√(K1+K2)K1K2C12π√kmD12π√K1K2m(K1+K2)
A12π√KmB12π√(K1+K2)K1K2C12π√kmD12π√K1K2m(K1+K2)The frequency of oscillation of the spring shown in the figure will be
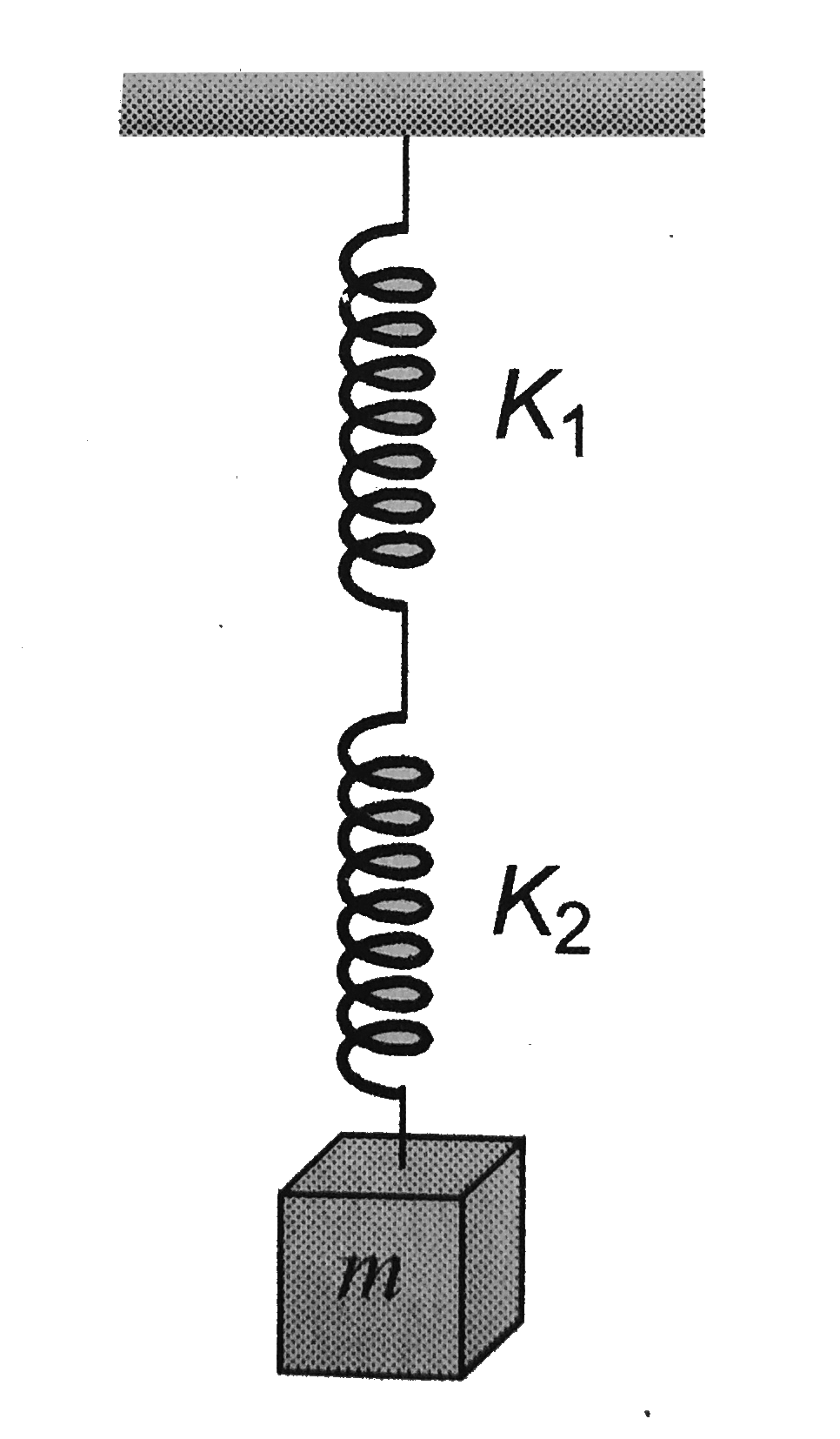 A12π√KmB12π√(K1+K2)mK1K2C2π√KmD12π ⎷(K1K2m(K1+K2))
A12π√KmB12π√(K1+K2)mK1K2C2π√KmD12π ⎷(K1K2m(K1+K2))
A mass m is suspended from a spring of length l and force constant K . The frequency of vibration of the mass is f1. The spring is cut into two equal parts and the same mass is suspended from one of the parts. The new frequency of vibration of mass is f2 . Which of the following relations between the frequencies is correct
View SolutionThe frequency of oscillations of a mass m connected horizontally by a spring of spring constant k is 4 HZ. When the spring is replaced by two identical spring as shown in figure. Then the effective frequency is

View SolutionSome springs are combined in series and parallel arrangement as shown in the figure and a mass m is suspended from them. The ratio of their frequencies will be
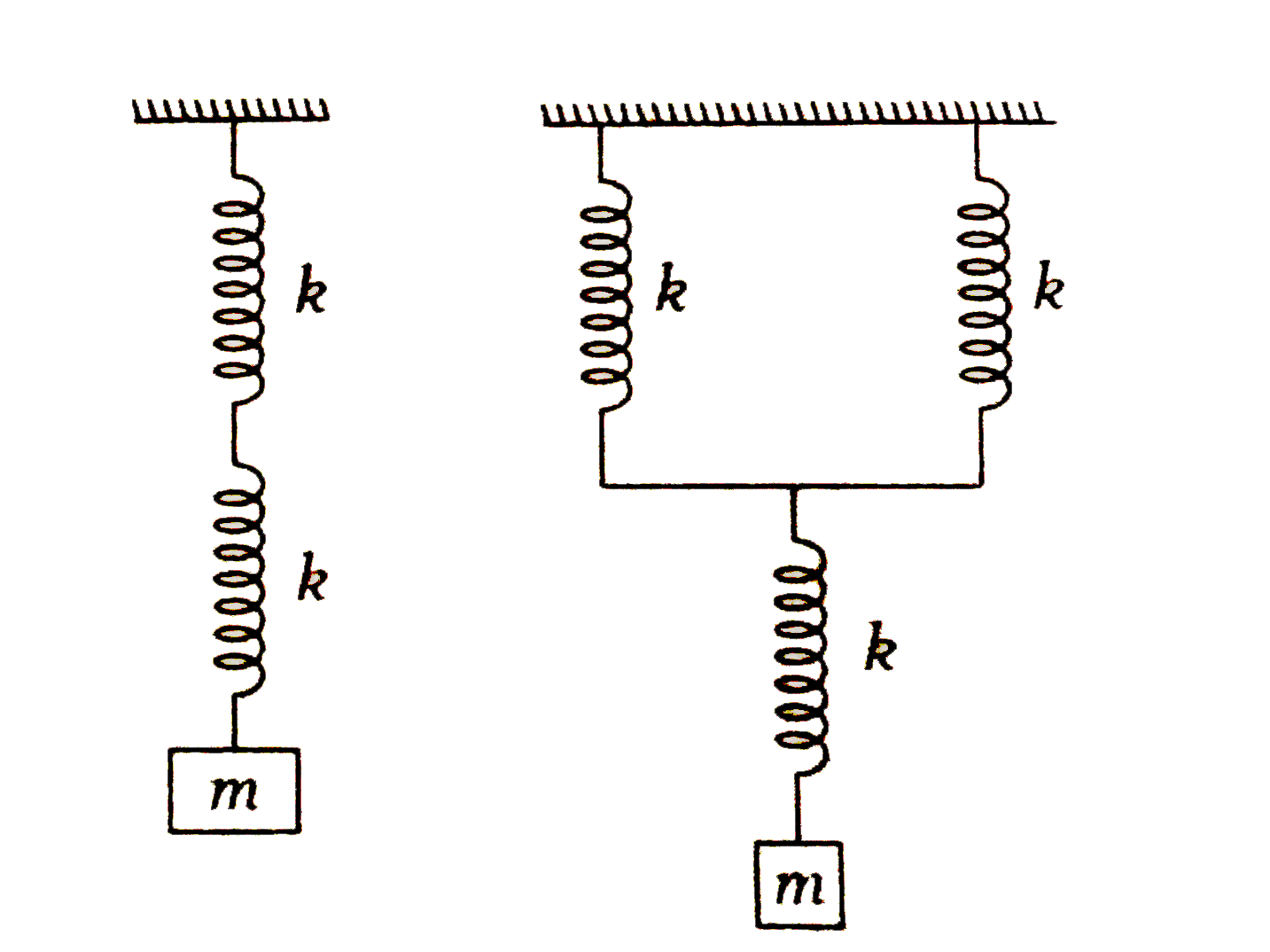
View SolutionSome springs are combined in series and parallel arrangement as shown in the figure and a mass m is suspended from them. The ratio of their frequencies will be :-
_E01_040_Q01.png)
View SolutionA mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is

View Solution