यंग के द्विस्लिट प्रयोग में एक स्लिट, दूसरे की अपेक्षा चौड़ी है जिससे एक स्लिट के प्रकाश का आयाम, दूसरे की अपेक्षा दोगुना है | यदि अधिकतम तीव्रता Im है तो कलान्तर ϕ होने पर परिणामी तीव्रता I का मान होगा :
Im9(4+5cosϕ)
Im3(1+2cos2π2)
Im5(1+4cos2ϕ2)
Im9(1+8cos2ϕ2)
The correct Answer is:D
प्रश्नानुसार, a1=2a2∴ यदि I1=I0 तो I2=4I0 तथा I=I1+I2+2√I1I2cosϕ=I0+4I0+2√I0×4I0cosϕ
या I=5I0+4I0cosϕ ...(i) अब ϕ=0 पर Im=9I0 ...(iii)
समीकरण (ii) से, I0=Im/9 लिखने पर समीकरण (iii) से, I=Im9(1+8cos2ϕ2)
Topper's Solved these Questions
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - तरंग प्रकाशिकीEXERCISE - आंकिक प्रश्न10videos
तरंग प्रकाशिकी
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - चुम्बकत्व एवं द्रव्य EXERCISE - इन्जीनियरिंग एवं मेडिकल की विभिन्न प्रतियोगी प्रवेश परीक्षाओ के लिए ( वस्तुनिष्ट प्रश्न )72videos
चुम्बकत्व एवं द्रव्य
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - द्रव्य तथा विकिरण की द्वैती प्रकृति EXERCISE - वस्तुनिष्ठ प्रश्न80videos
द्रव्य तथा विकिरण की द्वैती प्रकृति
Similar Questions
चित्र 10.36 में तीव्रता I का एक संकीर्ण एकवर्णी प्रकाश पुंज काँच की एक प्लेट पर आपतित होता है | एक दूसरी समरूप प्लेट, पहली प्लेट के पास उसके समान्तर रखी गयी है | प्रत्येक प्लेट, इस पर आपतित प्रकाश का 25% भाग परावर्तित तथा शेष भाग पारगमित करती है | दोनों प्लेटों से परावर्तन के फलस्वरूप प्राप्त व्यतिकरण प्रतिरूप में न्यूनतम तथा अधिकतम तीव्रता का अनुपात ज्ञात कीजिए |
09:58View Solutionचुम्बकीय क्षेत्र B की क्षेत्र रेखाओ से संबंधित कथन नहीं है
04:33View Solutionकैथोड किरणों पर आवेश होता है :
06:02View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
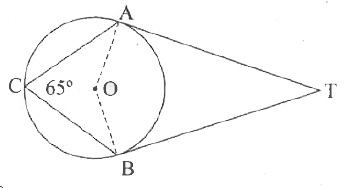
04:01View Solutionसंलग्न आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक - दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा:
 02:10View Solution
02:10View Solutionसंल्गन आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक -दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा -
 05:14View Solution
05:14View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।02:32View Solutionयदि शब्द PROBABILITY के अक्षर एक पंक्ति में यदृच्छया लिखे जाते है तो दो के साथ आने की प्रायिकता है -
01:23View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
56:15View Solutionयदि द्विघात समीकरण 81x2+kx+256=0 का एक मूल दूसरे मूल का घन है , तो k का एक मान है
01:31:03View Solutionयदि बिंदु (3,4) समीकरण 3y=ax+6 के आलेख पर स्थित है , तो a का मान होगा :
29:26View Solutionयंग का द्वीस्लिट प्रयोग|विवर्तन तथा एकल स्लिट प्रयोग
01:14:37View Solutionव्यतिकरण|यंग का स्लिट प्रयोग
View Solutionयंग का द्वि स्लिट प्रयोग
37:32View Solutionयंग का द्वि- स्लिट प्रयोग#!#यंग का एकल झिरी प्रयोग
View Solutionयंग का द्वि-स्लिट प्रयोग#!#विवर्तन
View Solution

