In Fig. 7.150 , coefficient of friction between m2 and the horizontal surface is μ , minimum value of m so that the system has zero acceleration , is :

μ(m1+m2)
μ(m1+m2)
m2−m1μ
m1μ−m2
The correct Answer is:D
For zero acceleration ,
Pulling force = Frictional force
m1g=μ(m2+m)g
m1=μ(m2+m)
m1μ−m2=m
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - More than one correct18videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Assertion - Reason12videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Problem For Practice23videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension12videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston14videos
MOTION IN A STRAIGHT LINE
Similar Questions
Two blocks of mass 'm' and 'M, are connect to the ends of a string passing over a pulley. 'M' lies on the plane inclined at an angle θ with the horizontal and 'm' is hanging vertically as shown in Fig. The coefficient of static friction between 'M' and the incline is μs. Find the minimum and maximum value of 'm' so that the system is at rest.
 View Solution
View SolutionWhen force F applied on m2 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ… What should be the minimum value of F so that there is no relative motion between m1andm2
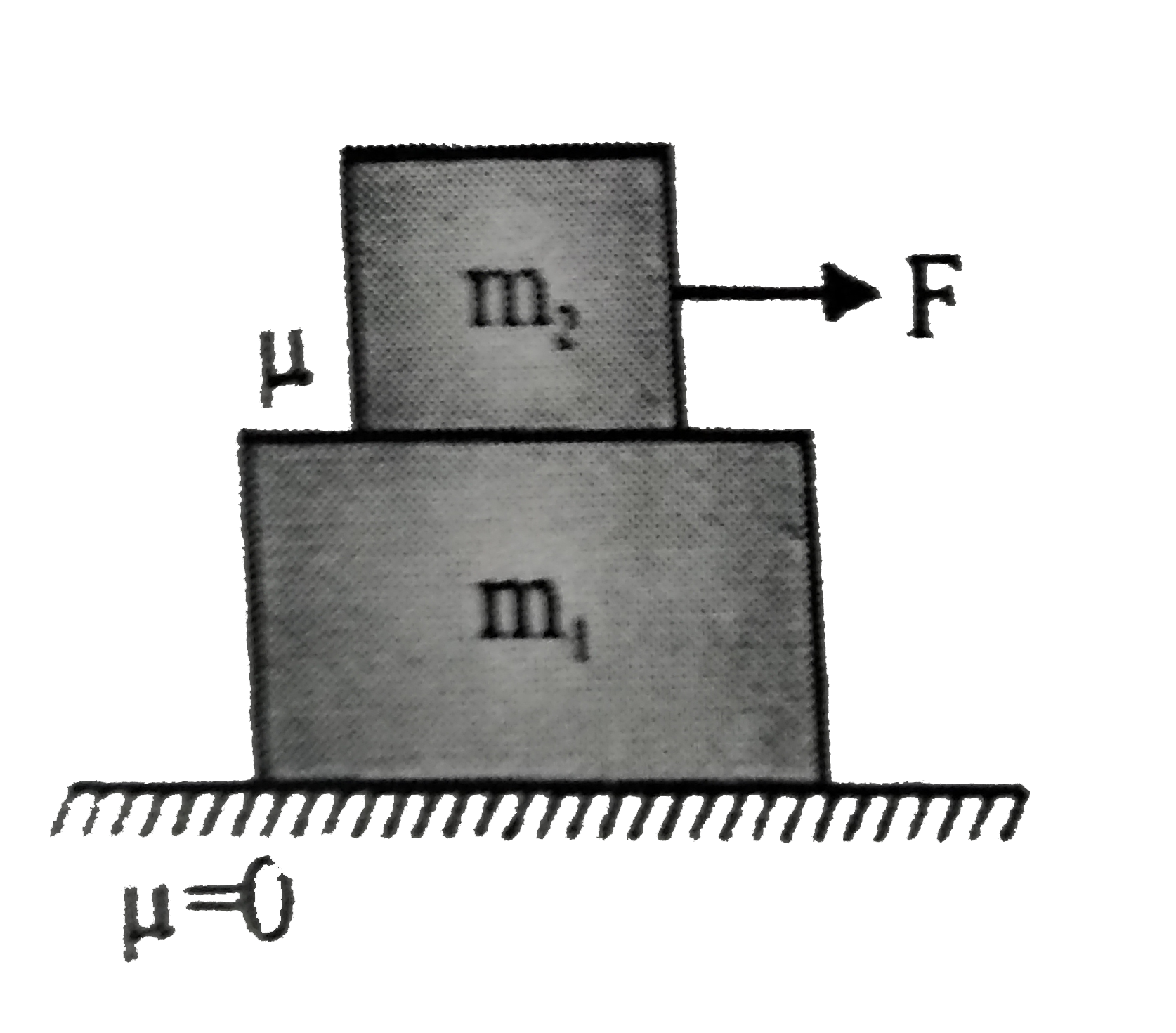 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 A75μmgB47μmgC57μmgD72μmg
A75μmgB47μmgC57μmgD72μmg - Question 2 - Select One
A plank of mass 3m is placed on a rough inclined plane and a man of mass m, the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of man so that plank does not slide is :
 A8m/s2B4m/s2C6m/s2D3m/s2
A8m/s2B4m/s2C6m/s2D3m/s2 - Question 3 - Select One
A trolley of mass M is attached to a block of mass m by a string passing over a frictionless pulley as shown in the figure. If the coefficient of friction between the horizontal surface and wheels of trolley is μ, then acceleration of the block m and that of trolley M on releasing the system is :-
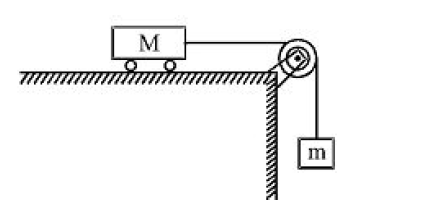 A(μM−mm+μM)gB(m+μMμM−m)gC(μm−Mm+M)gD(m−μMm+M)g
A(μM−mm+μM)gB(m+μMμM−m)gC(μm−Mm+M)gD(m−μMm+M)g
When force F applied on m1 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is on relative motion between m1andm2
 View Solution
View SolutionWhen force F applied on m1 and surface. Is μ1 and the coefficient of friction between m1andm2 is μ2. What should be the minimum value of F so that there is no relative motion between m1andm2.
 View Solution
View SolutionIf the coefficient of friction between M and the inclined surfaces is μ=1/√3 find the minimum mass m of the rod so that the of mass M=10kg remain stationary on the inclined plane
 View Solution
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
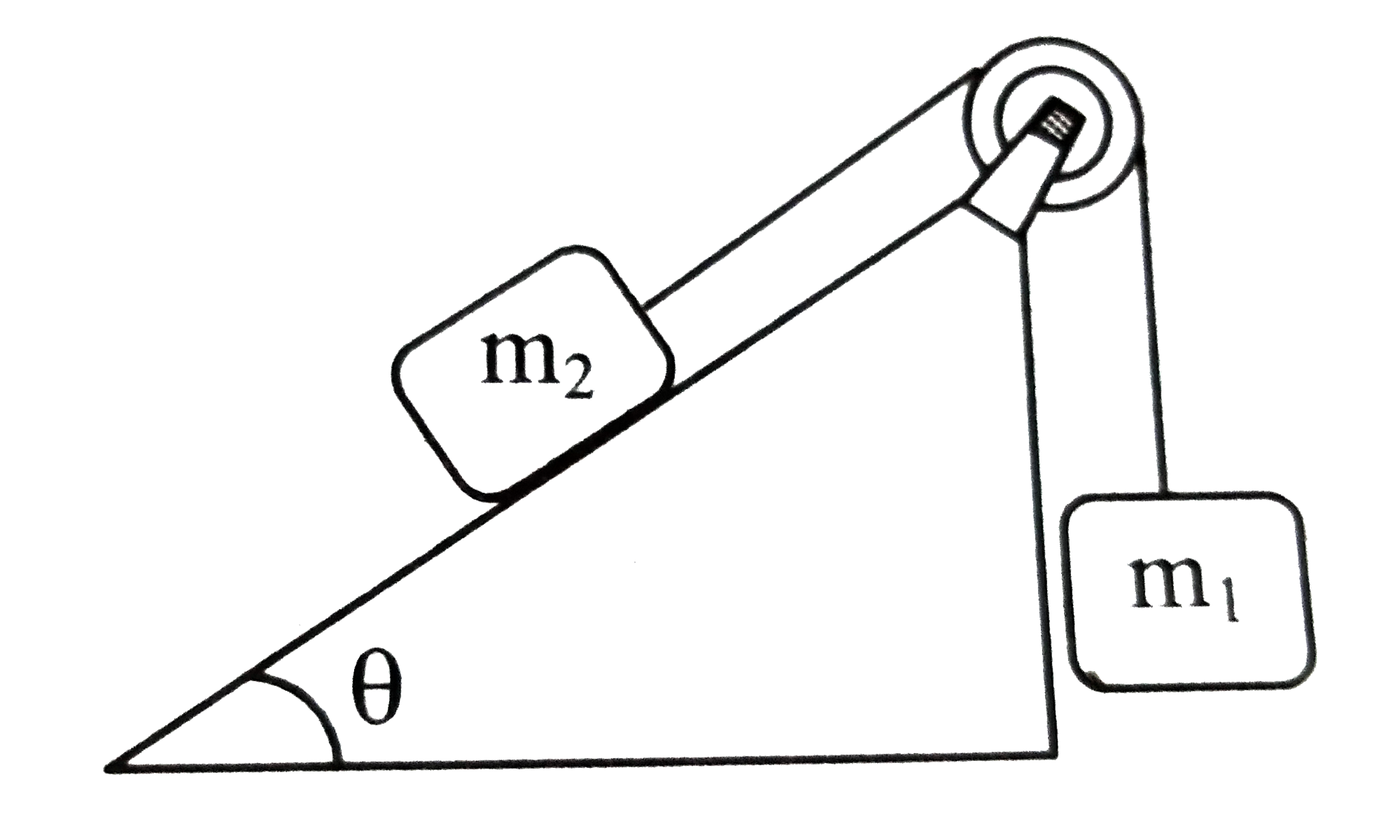 View Solution
View SolutionIn the figure, m1=m2=10kg. The coefficients of friction between A,B and B, surface are 0.2. Find the maximum value of m3 so that no block slips ( All the pullies are ideal and strings are massless).
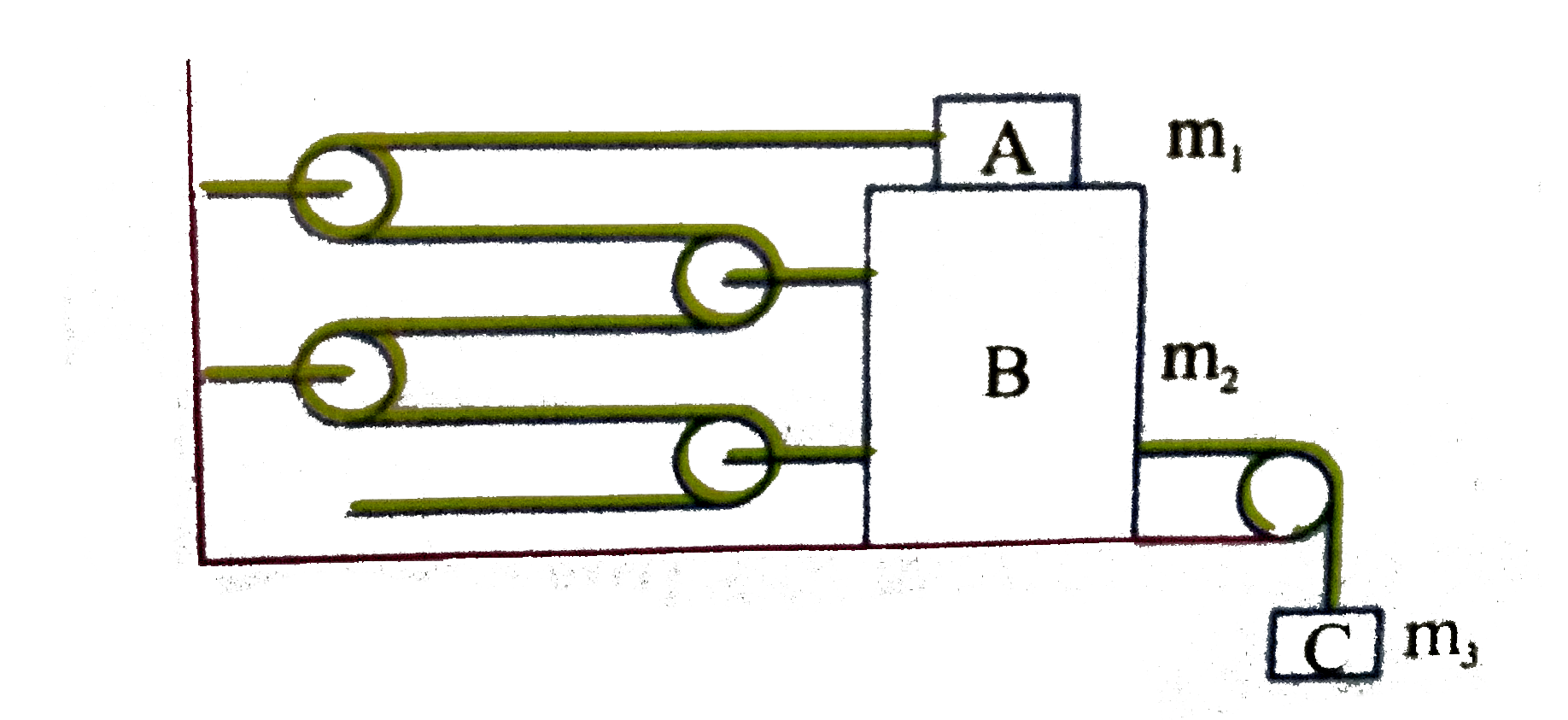 View Solution
View Solution

