What is the maximum possible area of a triangle with a side of length 7 units and another side of length 8 units?
To find the maximum possible area of a triangle with sides of lengths 7 units and 8 units, we can follow these steps:
Step 1: Understand the Triangle Area Formula
The area A of a triangle can be calculated using the formula:
A=12×base×height
Step 2: Identify the Given Sides
We are given two sides of the triangle:
- Side 1 (length a) = 7 units
- Side 2 (length b) = 8 units
Step 3: Determine the Configuration for Maximum Area
To maximize the area of a triangle with two given sides, the triangle should be a right triangle. This is because the area is maximized when the two sides are perpendicular to each other, with one side acting as the base and the other as the height.
Step 4: Assign Base and Height
Let’s assign:
- Base = 8 units
- Height = 7 units
Step 5: Calculate the Area
Now, we can substitute the values into the area formula:
A=12×8×7
Calculating this gives:
A=12×56=28 square units
Conclusion
The maximum possible area of the triangle with sides of lengths 7 units and 8 units is:
28 square units
---
The area A of a triangle can be calculated using the formula:
A=12×base×height
We are given two sides of the triangle:
- Side 1 (length a) = 7 units
- Side 2 (length b) = 8 units
To maximize the area of a triangle with two given sides, the triangle should be a right triangle. This is because the area is maximized when the two sides are perpendicular to each other, with one side acting as the base and the other as the height.
Let’s assign:
- Base = 8 units
- Height = 7 units
Now, we can substitute the values into the area formula:
A=12×8×7
Calculating this gives:
A=12×56=28 square units
The maximum possible area of the triangle with sides of lengths 7 units and 8 units is:
28 square units
Similar Questions
Knowledge Check
Find the area of an equilateral triangle with a side length of 12
A6√3B18√3C36√3D72√3A triangle is not possible with sides of length (in cm)
A6,4,10B5,3,7C7,8,9D3.6,5.4,8
Construct an isosceles triangle with equal sides of length 6 cm each and the base of length 7 cm.
View SolutionWhat is the greatest possible perimeter of a right angled triangle with integer side lengths if one of the sides has length 12?
View SolutionTwo sides of a triangle have lengths of 5 and 19. Can the third side have a length of 13?
View SolutionLet the point P lies in the interior of an equilateral triangle with side lengths 2 units, each. Find the sum of the shortest distances from P to the sides of the triangle.
View SolutionThe lengths of the side of ΔABC are consecutive integers. It ABC has the same perimeter as an equilateral triangle triangle with a side of length 9cm, what is the length of the shortest side of ABC ? 4 (b) 6 (c) 8 (d) 10
View Solution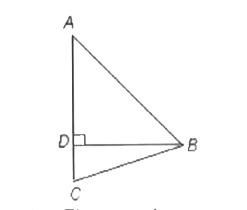
Triangle ABC has the same area as a rectangle with sides of lengths 5 and 7. If the length of ¯¯¯¯¯¯AC is 10, what is the length of ¯¯¯¯¯¯BD?
View Solution
