What is the longest diagonal of a rectangular box that is 120 inches long, 90 inches wide, and 80 inches tall?
To find the longest diagonal of a rectangular box (cuboid) with given dimensions, we can follow these steps:
Step 1: Identify the dimensions of the cuboid
The dimensions of the rectangular box are:
- Length (L) = 120 inches
- Width (B) = 90 inches
- Height (H) = 80 inches
Step 2: Use the formula for the diagonal of a cuboid
The formula for the longest diagonal (D) of a cuboid is given by:
D=√L2+B2+H2
Step 3: Substitute the dimensions into the formula
Substituting the values of L, B, and H into the formula:
D=√(120)2+(90)2+(80)2
Step 4: Calculate the squares of the dimensions
Now, calculate the squares:
- (120)2=14400
- (90)2=8100
- (80)2=6400
Step 5: Add the squared values
Now, add these squared values together:
14400+8100+6400=28900
Step 6: Take the square root of the sum
Now, take the square root of the sum to find the diagonal:
D=√28900
Step 7: Calculate the square root
Calculating the square root:
D=170
Final Answer
The longest diagonal of the rectangular box is:
D=170 inches
---
The dimensions of the rectangular box are:
- Length (L) = 120 inches
- Width (B) = 90 inches
- Height (H) = 80 inches
The formula for the longest diagonal (D) of a cuboid is given by:
D=√L2+B2+H2
Substituting the values of L, B, and H into the formula:
D=√(120)2+(90)2+(80)2
Now, calculate the squares:
- (120)2=14400
- (90)2=8100
- (80)2=6400
Now, add these squared values together:
14400+8100+6400=28900
Now, take the square root of the sum to find the diagonal:
D=√28900
Calculating the square root:
D=170
The longest diagonal of the rectangular box is:
D=170 inches
Similar Questions

In the figure above, a rectangular container with the dimensions 10 inches by 15 inches by 20 inches is to be filled with water, using a cylindrical cup whose radius is 2 inches and whose height is 5 inches. What is the maximum number of full cups of water that can be placed into the container without the water overflowing the container?
View SolutionFind the perimeter of a table 34.5 inches wide and 58.5 inches long.
View Solution
Knowledge Check
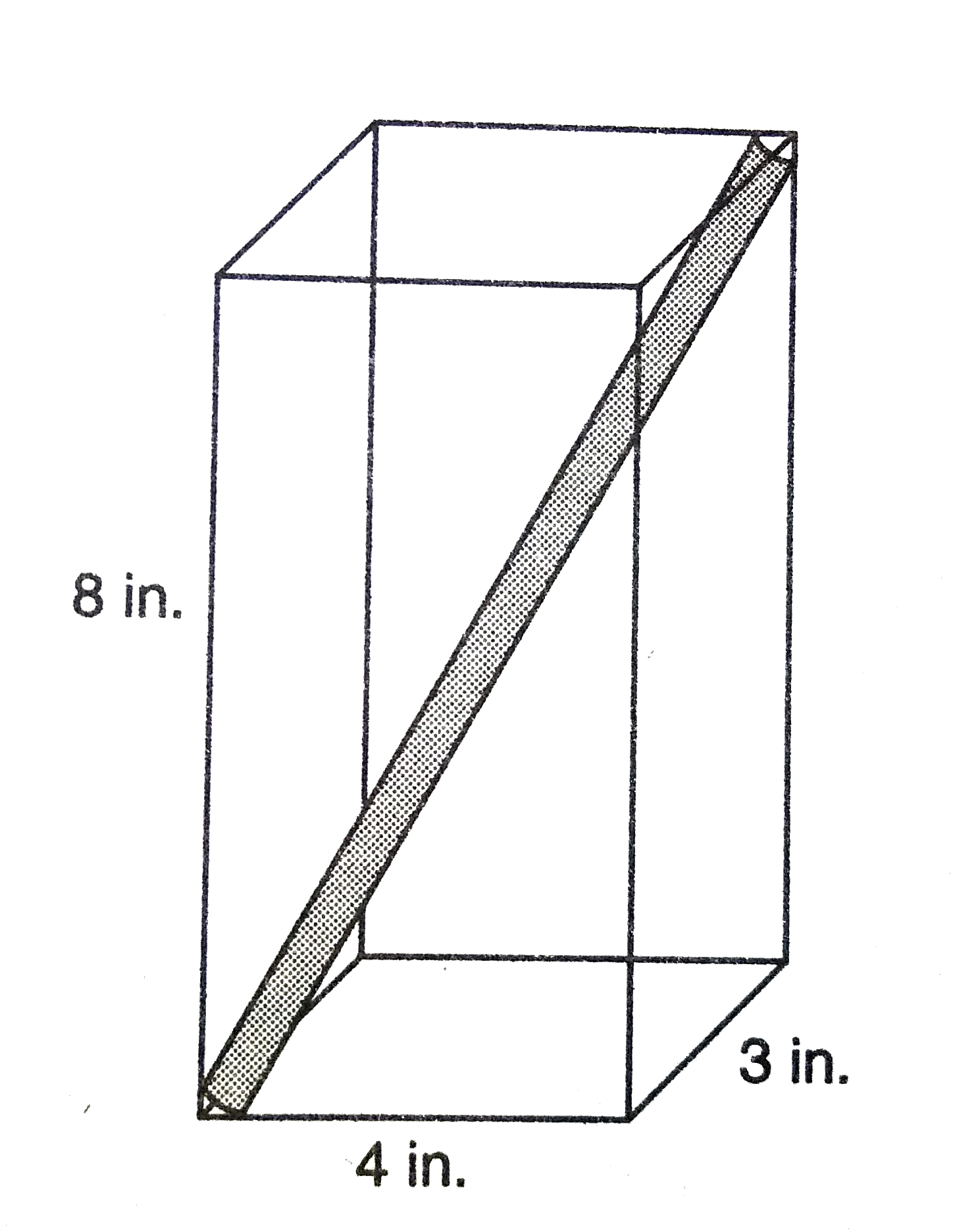
A cylindrical tube with ngligible thichness is placed into a rectangular box that is 3 inches by 4 inches by 8 inches, as shown in the accompanying diagram. If the tubes fits exactly into the box diagonally from the bottom left corner to the top right back corner, what is the best approximately of the number of inches in the length of the cube?A3.9B5.5C7.8D9.4A company ships notepads in rectangular boxes that each have inside dimensions measuring 9 inches long, 9 inches wide, and 12 inches tall. Each notepad is in the shape of a cube with an edge length of 3 inches. What is the maximum number of natepads that will fit in 1 closed box?
A10B11C12D36Find the length of the longer diagonal of a parallelogram if the sides are 6 inches and 8 inches and the smaller angle is 60∘
A8B11C12D7
The painting The starry night by vincent van gogh is rectangular in shape with height 29 inches and width 36.25 inches. IF a reproduction was made where each dimensions is 13 the corresponding original dimension, what is the height of the reproduction , in inches?
View SolutionMilk is poured from a full rectangular container with dimensions 4 inches by 9 inches by 10 inches into cylindrical container with a diameter of 6 inches. Assuming all the milk is transferred without spilage, how many inches high will the milk reach in the cylindrical container?
View SolutionBarb is going to cover a rectangular area 8 feet by 10 feet with rectangular paving blocks that are 4 inches by 8 inches by 2 inches to make a flat patio. What is the minimum number of paving blocks she will need if all the paving blocks will face the same direction?
(Note: Barb will not cut any of the paving blocks.)
View SolutionKen baked, frosted, and decorated a rectangular cake for the last Math Club meeting. The cake was 3 inches high, 12 inches wide, and 16 inches long. He centrated the cake on a piece of carboard whose rectangular top surface had been covered with aluminum foil, as shown in the figure below.
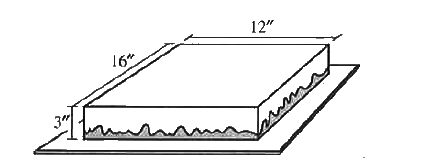
Ken used a piece of cardboard large enough to allow the cardboard to extend 2 inches beyond the cake on all sides. What is the area, in square inches, of the aluminum foil that is exposed on the top surface of the cardboard?
View SolutionThe length of a rectangular banner is 3 feet 2 inches, and the width is 2 feet 4 inches. Which one of the following equals the area of the banner?
View Solution
